Математика, вопрос задал Аноним , 6 лет назад

Найти область сходимости степенного ряда.

Приложения:

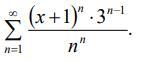
Ответы на вопрос

Ответил NNNLLL54

1

Ответ:

$\displaystyle \sum \limits _{n=1}^{\infty }\frac{(x+1)^{n}\cdot 3^{n-1}}{n^{n}}\\\\\\ \lim\limits_{n \to \infty}\, \frac{|u_{n+1}|}{|u_{n}|}=\lim\limits_{n \to \infty}\, \frac{|x+1|^{n+1}\cdot 3^{n}}{(n+1)^{n}(n+1)}\cdot \frac{n^{n}}{|x+1|^{n}\cdot 3^{n-1}}=\\\\\\=\lim\limits_{n \to \infty}\, \frac{3\cdot |x+1|}{n+1}\cdot \Big(\frac{n}{n+1}\Big)^{n}=\lim\limits_{n \to \infty}\, \frac{3\cdot |x+1|}{n+1}\cdot \Big(1-\frac{1}{n+1}\Big)^{n}=$

$\displaystyle =3\cdot |x+1|\cdot \lim\limits_{n \to \infty}\, \frac{e^{-1}}{n+1}=0<1\ \ \ pri\ \ \ \forall \, x\\\\\\Oblast\ sxodimosti\ \ x\in R$

Аноним: спасибо еще раз!
а можешь еще это, последнее на сегодня, пожалуйста!
https://znanija.com/task/46615894

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

почему в слове ключом пишется буква о...

Қазақ тiлi, 1 год назад

максат багынкылы сабактас курмалас сойлем...

Русский язык, 6 лет назад

сочинение рассуждение на тему хобби может стать зароботком...

Українська мова, 6 лет назад

скласти твір про останні місяці осені срочно поможіть будь ласка...

Физика, 8 лет назад

Планетарное строение атома аналогично строению Солнечной системы. В чём различия между этими моделями?

Математика, 8 лет назад

4860-k•62=2442 помогите решить уравнение...