Алгебра, вопрос задал sawa0000 , 7 лет назад

найти наибольшее и наименьшее значение функции на отрезке [-5;5]
Помогите пожалуйста!

Приложения:

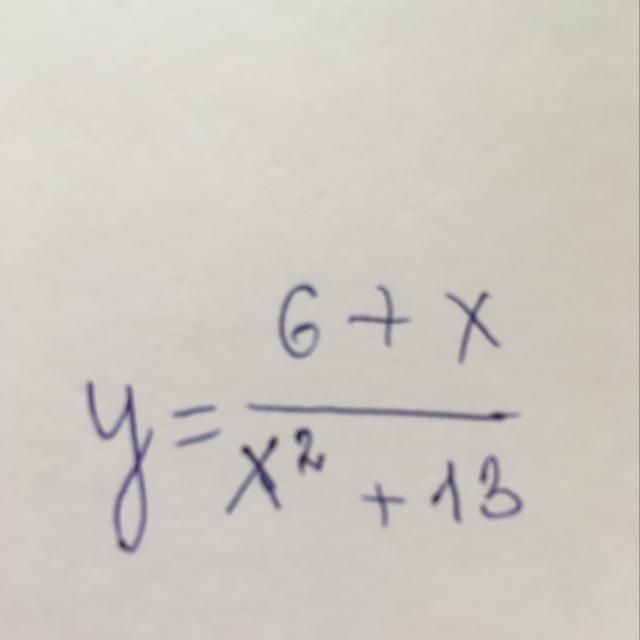
Ответы на вопрос

Ответил Dushzhanov987

$displaystyle y=frac{6+x}{x^2+13}; ;;;; boxed{(frac{u}{v})'=frac{u'v-v'u}{v^2}}\y'=frac{(x^2+13)-2x(6+x)}{(x^2+13)^2}=frac{x^2+13-12x-2x^2}{(x^2+13)^2}=frac{-x^2-12x+13}{(x^2+13)^2}; ; y'=0\-x^2-12x+13=0; ;;; x^2+12x-13=0;\ left { {{x_1x_2=-13} atop {x_1+x_2=-12}} right. left [{ {{x=-13} atop {x=1}} right. ;\ +++[-5]+++(1)---[5]--->x$

$tt x=1 - maximum; ;;; y(1)=frac{7}{14}=0,5\ \x=5 - minimum; ;;; y(5)=frac{11}{38}$

Наибольшее значение ф-ции: y=0,5

Наименьшее значение ф-ции: $y=frac{11}{38}$

Ответил Crazymadstudent

Ответ:

max=1/2

min= -6/157

Объяснение: Для того чтобы найти эти значения нужно сначала подставить числа 5 и -5,

А далее рассмотреть экстремумы функции, тоесть взять прозводную и приравнять к нулю, тогда получите ответ, в нашем случае два ответа и эти два корня нужно также подставить и получить ответ

Приложения: