найти наибольшее и наименьшее значение функции f(x)=3x-x³ [-3;0]
Ответы на вопрос
Ответил agasikkk
0
f(x)=3x-x³
Находим производную
f ' (x) = 3-3x²
Приравнием у нулю 3-3х²=0 -3х²=-3 х²=1. х=1 х=-1 у нас дано промежуток (-3:0) +1 туда не входит
подставляем цифры эти в начало уравнения
f(-3)=-9+27=18
f(0)=0
f(-1)=-3+1=-2 Наименьшее равно f(-1)= -2 min
Находим производную
f ' (x) = 3-3x²
Приравнием у нулю 3-3х²=0 -3х²=-3 х²=1. х=1 х=-1 у нас дано промежуток (-3:0) +1 туда не входит
подставляем цифры эти в начало уравнения
f(-3)=-9+27=18
f(0)=0
f(-1)=-3+1=-2 Наименьшее равно f(-1)= -2 min
Ответил dasdasfa
0
Класс! Только -не подставляем, а найдём значения функции при х=-1; х=0; х=-3)!
Ответил agasikkk
0
ну да это так,но кто задание задал,ему легче понять будет)
Ответил Anastsiia
0
Убывает от
Возрастает на
Наибольшее значение
Наименьшее значение
Приложения:

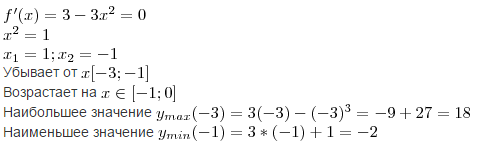
Ответил agasikkk
0
Можно вопрос,вот вы картинки загрузили,на каком сайте можно писать?
Ответил Anastsiia
0
Какие картинки? Если ты за скриншот решения, он написан в макропакете Lateh, ты когда задание/ответ пишешь, там есть буква/значек П - при его нажатии можно писать адекватные формулы и не мучаться
Ответил agasikkk
0
спасибо
Новые вопросы