Найти корень уравнения. В случае, если их несколько, найти их сумму.
Приложения:
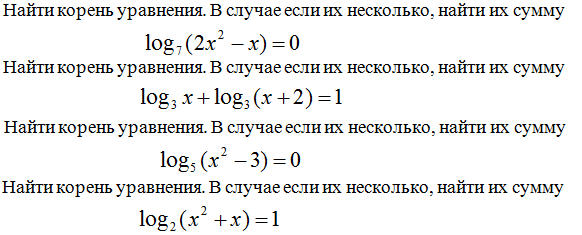
Ответы на вопрос
Ответил Аноним
0
1. ОДЗ: 



x=-3 - не удовлетворяет ОДЗ
Ответ: 1.


x=-3 - не удовлетворяет ОДЗ
Ответ: 1.
Ответил Аноним
0
1)2x²-x>0
x(2x-1)>0
x=0 U x=1/2
x∈(-∞;0) U (1/2;∞)
2x²-x=1
2x²-x-1=0
D=1+8=9>0
x1+x2=1/2
2)x>0 U x-2>0⇒x>2
x∈(2;∞)
log(3)[x*(x-2)]=1
x²-2x=3
x²-2x-3=0
D=4+12=16>0
x1+x2=2
3)x²-3>0
x=-√3 U x=√3
x∈(-∞;-√3) U (√3;∞)
x²-3=1
x²=4
x1=-2 U x2=2
x1+x2=0
4)x²+x>0
x(x+1)>0
x=0 x=-1
x∈(-∞;-1) U (0;∞)
x²+x=2
x²+x-2=0
D=1+8=9>0
x1+x2=-1
x(2x-1)>0
x=0 U x=1/2
x∈(-∞;0) U (1/2;∞)
2x²-x=1
2x²-x-1=0
D=1+8=9>0
x1+x2=1/2
2)x>0 U x-2>0⇒x>2
x∈(2;∞)
log(3)[x*(x-2)]=1
x²-2x=3
x²-2x-3=0
D=4+12=16>0
x1+x2=2
3)x²-3>0
x=-√3 U x=√3
x∈(-∞;-√3) U (√3;∞)
x²-3=1
x²=4
x1=-2 U x2=2
x1+x2=0
4)x²+x>0
x(x+1)>0
x=0 x=-1
x∈(-∞;-1) U (0;∞)
x²+x=2
x²+x-2=0
D=1+8=9>0
x1+x2=-1
Новые вопросы
Алгебра,
1 год назад
Алгебра,
1 год назад
Химия,
1 год назад
Право,
1 год назад
Математика,
7 лет назад