Найти интеграл
dx/(sin^2xcos^2x)
Ответы на вопрос
Ответил bodan741
0
Интеграл на фото. Удачи
Приложения:
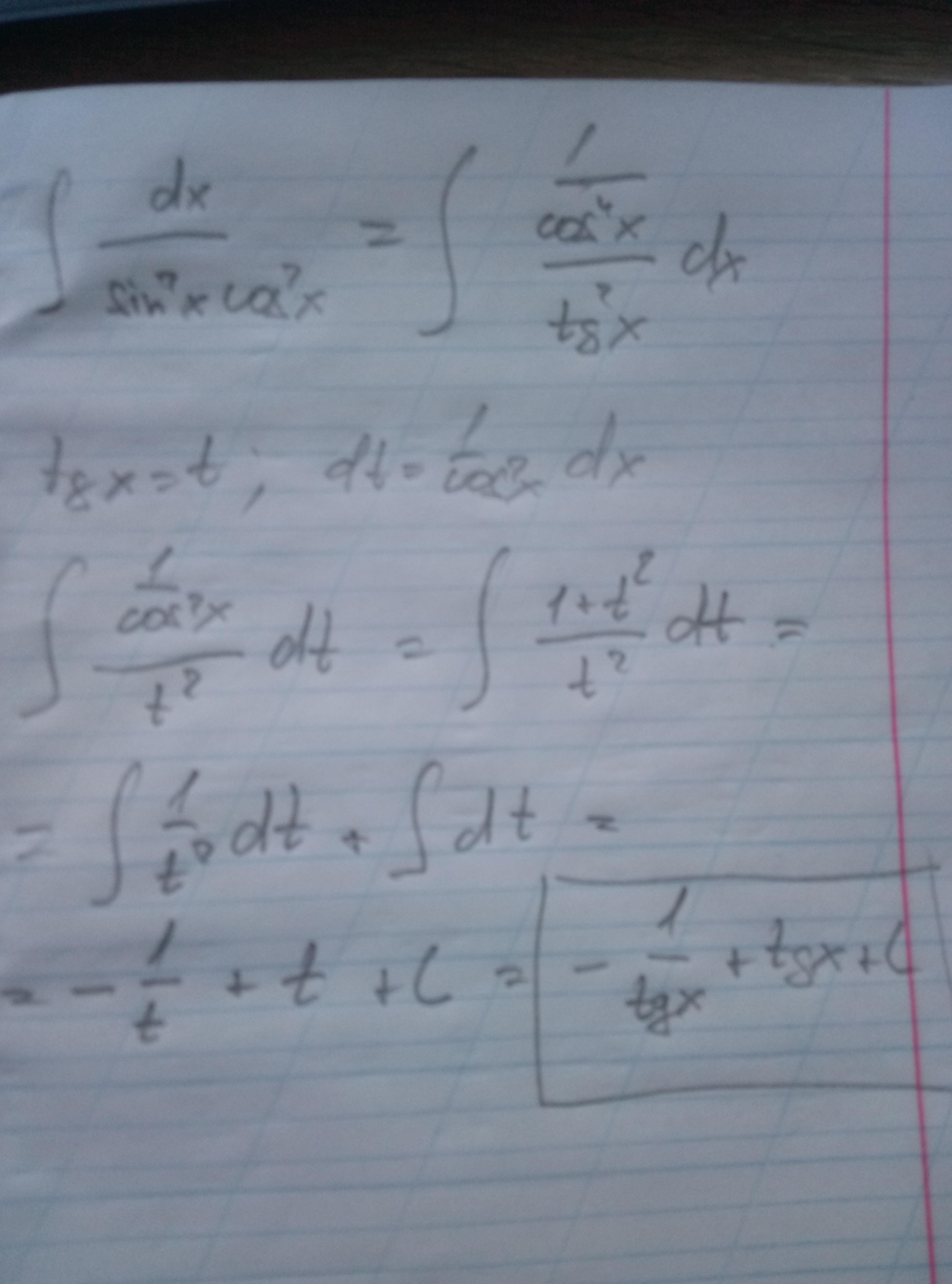
Ответил takushnir
0
Применим формулу синуса двойного аргумента 2sinx*cosx=sin2x, умножив на 4 числитель и знаменатель, в знаменателе получим sin²2x, и воспользуемся табличным интегралом ∫dx/sin²у=-сtgу+с, получим
∫dx/(sin²xcos²x)=4∫dx/(sin²2x)=2∫(d2x)/(sin²2x)=-2сtg2x+c;
Проверка (-2сtg2x+c)'=-2*(-1/sin²2x)*2=4/(4sin²x*cos²x)=1/(sin²xcos²x)
Приложения:
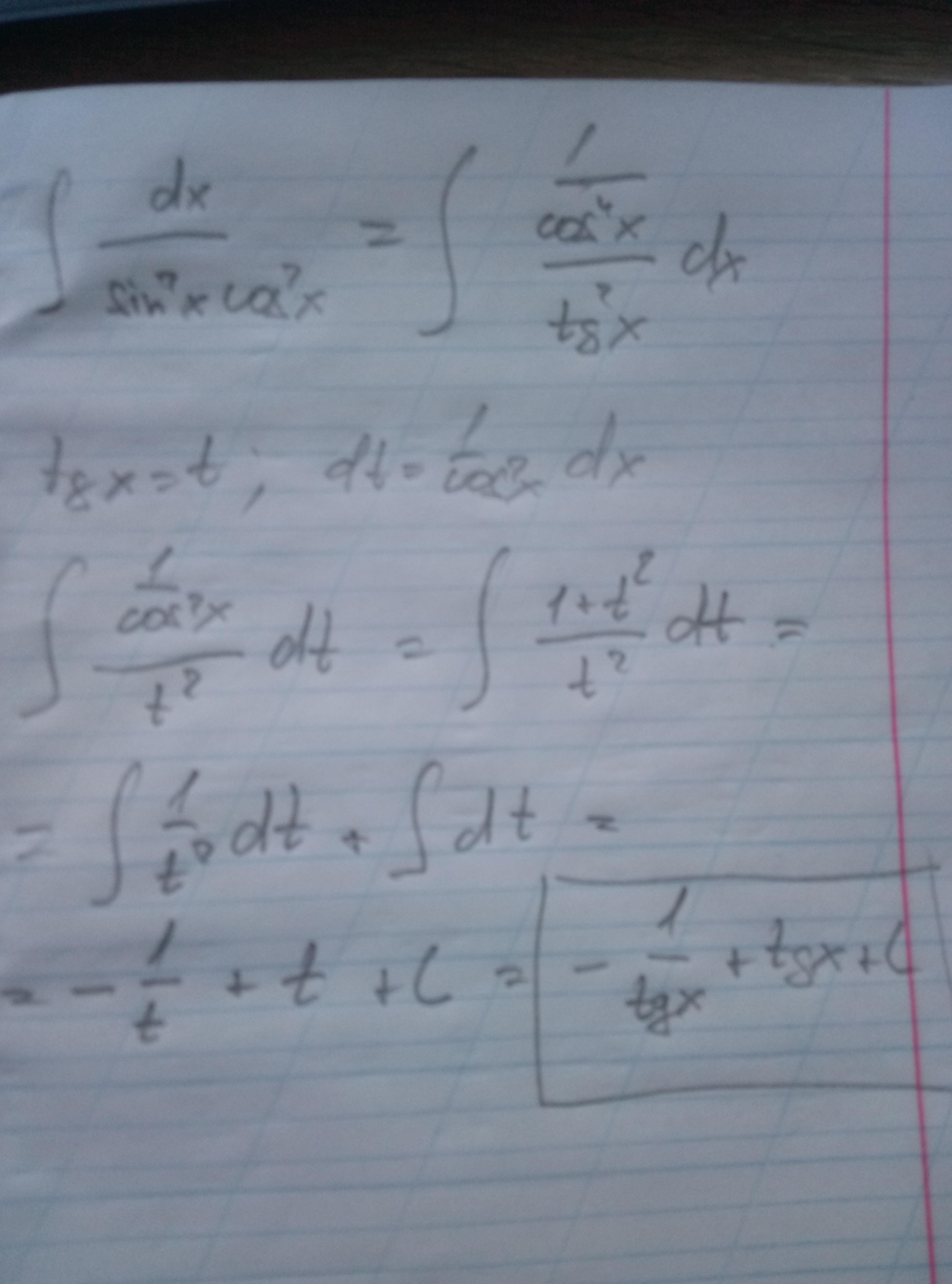
Новые вопросы
Английский язык,
1 год назад
Математика,
7 лет назад
Обществознание,
8 лет назад
Математика,
8 лет назад