Математика, вопрос задал osvalgwill , 6 лет назад

Найти интеграл........

Приложения:

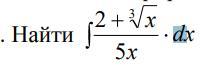
Ответы на вопрос

Ответил NNNLLL54
0

Ответ:

Метод замены переменной при интегрировании иррациональных выражений .

\displaystyle \int \frac{2+\sqrt[3]{x}}{5x}\, dx=\Big[\ x=t^3\ \ ,\ \ dx=3t^2\, dt\ ,\ t=\sqrt[3]{x}\ \Big]=\int \frac{(2+t)\cdot 3t^2\, dt}{5\, t^3}=\\\\\\=\frac{3}{5}\int \frac{2+t}{t}\, dt=\frac{3}{5}\int \Big(\frac{2}{t}+1\Big)\, dt=\frac{3}{5}\cdot \Big(2\, ln|\, t\, |+t\Big)+C=\\\\\\=\frac{3}{5}\cdot \Big(2\, ln\, |\sqrt[3]{x}\, |+\sqrt[3]{x}\Big)+C

Ответил Аноним
0

Ответ  ( 2/5)㏑IxI+(3∛x/5)+c

Пошаговое объяснение:

разделим почленно числитель на знаменатель.

(2+∛х)/(5х)=(2/(5х))+(х⁻²/³5)=(1/5)*((2/х)+(х⁻²/³5)

∫((1/5)*((2/х)+(х⁻²/³5))dx=(2/5)㏑IxI+3(x¹/³/5)+c=(2/5)㏑IxI+(3∛x/5)+c

Предыдущий вопрос
Следующий вопрос
Новые вопросы