Найти двугранный угол abcd
тэтраэдра abcd если углы dab dac acb прямые , ac=5=cb , db =5√5
Ответы на вопрос
Ответил Hrisula
0
Вспомним, что:
двугранным углом называется пространственная геометрическая фигура, образованная двумя полуплоскостями, исходящими из одной прямой.
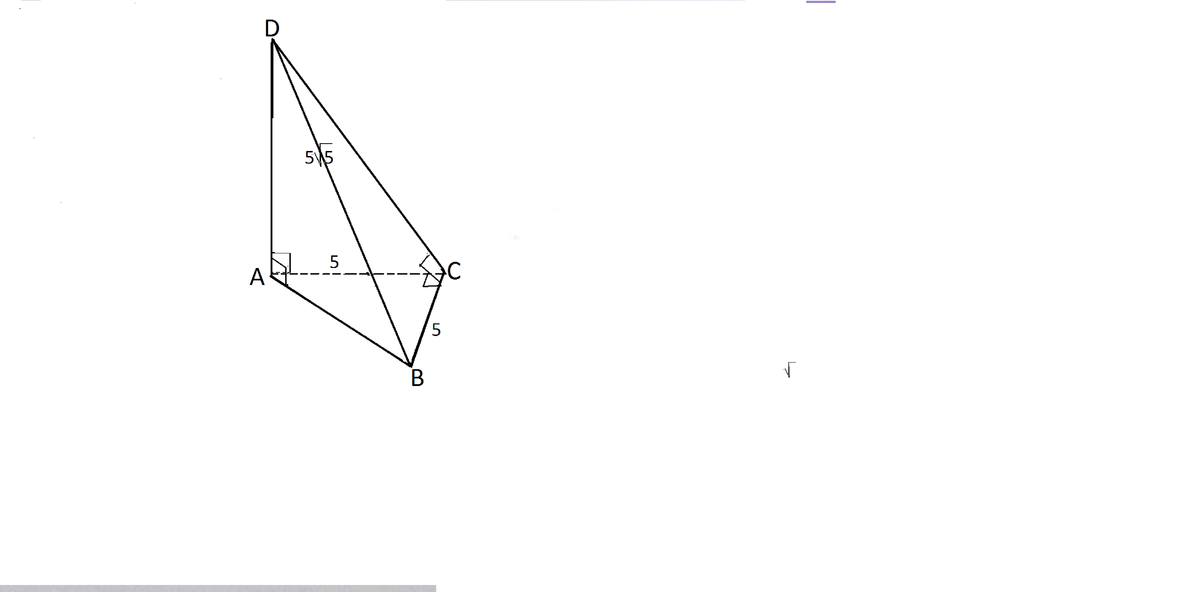
В нашем случае это полуплоскости DСВ и АСВ, а прямая ( ребро)- СВ.
Искомый двугранный угол - это угол между полуплоскостями DСВ и АСВ.
Величиной двугранного угла называется величина его линейного угла.
Линейный угол - это угол, образованный двумя лучами, которые имеют общее начало, лежащее на ребре двугранного угла, и проведенными в обеих гранях перпендикулярно ребру.
На рисунке это угол, образованный лучами DС и СА, которые имеют общее начало С, лежащее на ребре СВ двугранного угла.
DС перпендикулярна ребру СВ по теореме о трех перпендикулярах ( угол АСВ прямой по условию, АС - проекция наклонной DС, =>
гипотенуза DС треугольника DАС перпендикулярна ВС).
Следовательно, нужно найти величину угла DСА.
Косинус ∠ DСА=АС:DС
DС=√(DВ²-ВС²)=√(125-25)=10
cos ∠DСА= 5:10=1/2
∠DСА=60°
-------------------
[email protected]
двугранным углом называется пространственная геометрическая фигура, образованная двумя полуплоскостями, исходящими из одной прямой.
В нашем случае это полуплоскости DСВ и АСВ, а прямая ( ребро)- СВ.
Искомый двугранный угол - это угол между полуплоскостями DСВ и АСВ.
Величиной двугранного угла называется величина его линейного угла.
Линейный угол - это угол, образованный двумя лучами, которые имеют общее начало, лежащее на ребре двугранного угла, и проведенными в обеих гранях перпендикулярно ребру.
На рисунке это угол, образованный лучами DС и СА, которые имеют общее начало С, лежащее на ребре СВ двугранного угла.
DС перпендикулярна ребру СВ по теореме о трех перпендикулярах ( угол АСВ прямой по условию, АС - проекция наклонной DС, =>
гипотенуза DС треугольника DАС перпендикулярна ВС).
Следовательно, нужно найти величину угла DСА.
Косинус ∠ DСА=АС:DС
DС=√(DВ²-ВС²)=√(125-25)=10
cos ∠DСА= 5:10=1/2
∠DСА=60°
-------------------
[email protected]
Приложения:
Новые вопросы