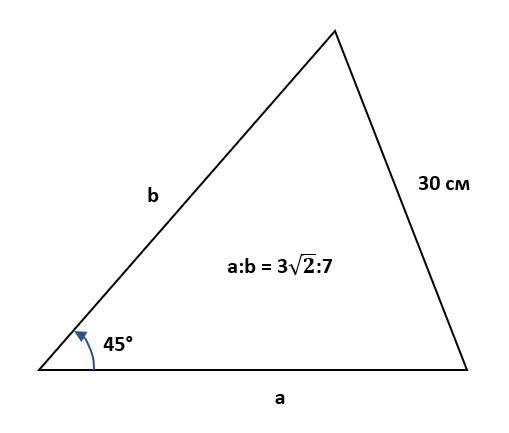
Найти большую сторону треугольника, если одна сторона равна 30см, а две другие относятся как 3√2: 7 и образуют угол 45°.

Ответ:

Большая сторона треугольника равна 42 см

Объяснение:

Дано:

  ΔABC (см. рисунок 1)

  c = AB = 30 см

  a:b = BC:AC = 3 : 7

  ∠C = 45°  

Найти: max{a; b; c}.

Решение. Известна теорема косинусов:

• Квадрат сторон треугольников равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними.

По теореме косинусов получим:

Объединив условие задачи и последнее равенство получим систему уравнений:

Учитывая, что a и b стороны треугольника, то есть a>0 и b>0, решим систему уравнений (см. рисунок 2).

Так как

42 > 30 и 42 > 18,

то ответом будет 42 см.

#SPJ1