Найдите высоту трапеции, боковые стороны которой равны 10 см и 17 см, а основы - 20 и 41 см.
Ответы на вопрос
Ответил kolobok1431
0
Дано:
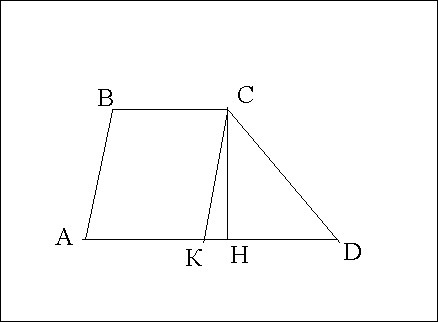
ABCD - трапеция
BC ║ AD
AB = 10 см
CD = 17 см
BC = 20 см
CD = 41 см
СН ⊥ СD
CH - h - высота
h - ?
Решение:
1) Проведем СК ║ АВ
В получившемся параллелограмме АВСК противоположные стороны равны:
АВ = СК = 10 см
ВС = КА = 20 см
2) Рассмотрим ΔCKD
CD = 17 см
CK = 10 см
KD = AD - KA = 41 - 20 = 21 см
Высота СН треугольника СКD является высотой данной трапеции.
3)А теперь найдём площадь ΔCKD по трем его сторонам по формуле Герона.

где р - полупериметр


 =84
=84
S = 84 cм²
4)
А теперь с помощью формулы площади треугольника через высоту

найдём высоту h

h = CK = 8 см
Ответ: 8 см.
ABCD - трапеция
BC ║ AD
AB = 10 см
CD = 17 см
BC = 20 см
CD = 41 см
СН ⊥ СD
CH - h - высота
h - ?
Решение:
1) Проведем СК ║ АВ
В получившемся параллелограмме АВСК противоположные стороны равны:
АВ = СК = 10 см
ВС = КА = 20 см
2) Рассмотрим ΔCKD
CD = 17 см
CK = 10 см
KD = AD - KA = 41 - 20 = 21 см
Высота СН треугольника СКD является высотой данной трапеции.
3)А теперь найдём площадь ΔCKD по трем его сторонам по формуле Герона.
где р - полупериметр
S = 84 cм²
4)
А теперь с помощью формулы площади треугольника через высоту
найдём высоту h
h = CK = 8 см
Ответ: 8 см.
Приложения:
Новые вопросы