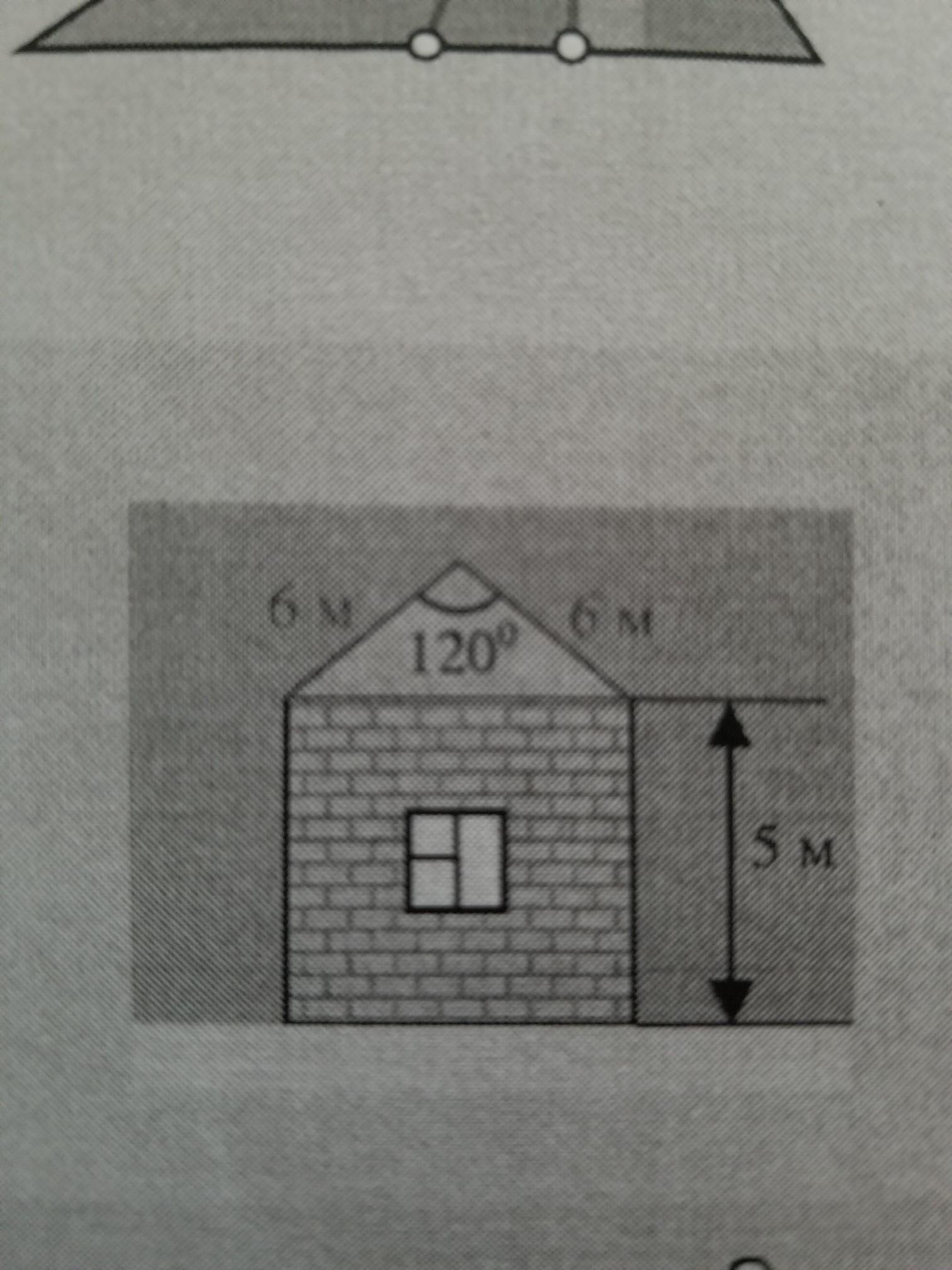
Найдите высоту дома, размеры которого показаны на рисунке, если угол между скатами его крыши равен 120 градусов.
Приложения:
Ответы на вопрос
Ответил ssuper99999
0
Проведём высоту из вершины треугольника на её противоположную сторону, тогда если треугольник равнобедренный (основания равны), то эта высота будет являться медианой и биссиктриссой, что делит угол на два равных(60°), при этом образовалось два равных прямоугольных треугольника, а значит углы при основании равны 30°. Мы знаем, что против угла лежит катет равный половине гипотенузы, то высота крыши равна 3м. Зная высоту дома и крыши, сложили их и найдём высоту самого дома: 3м+5м=8м
Ответ:8 м
Ответил Nekit455
0
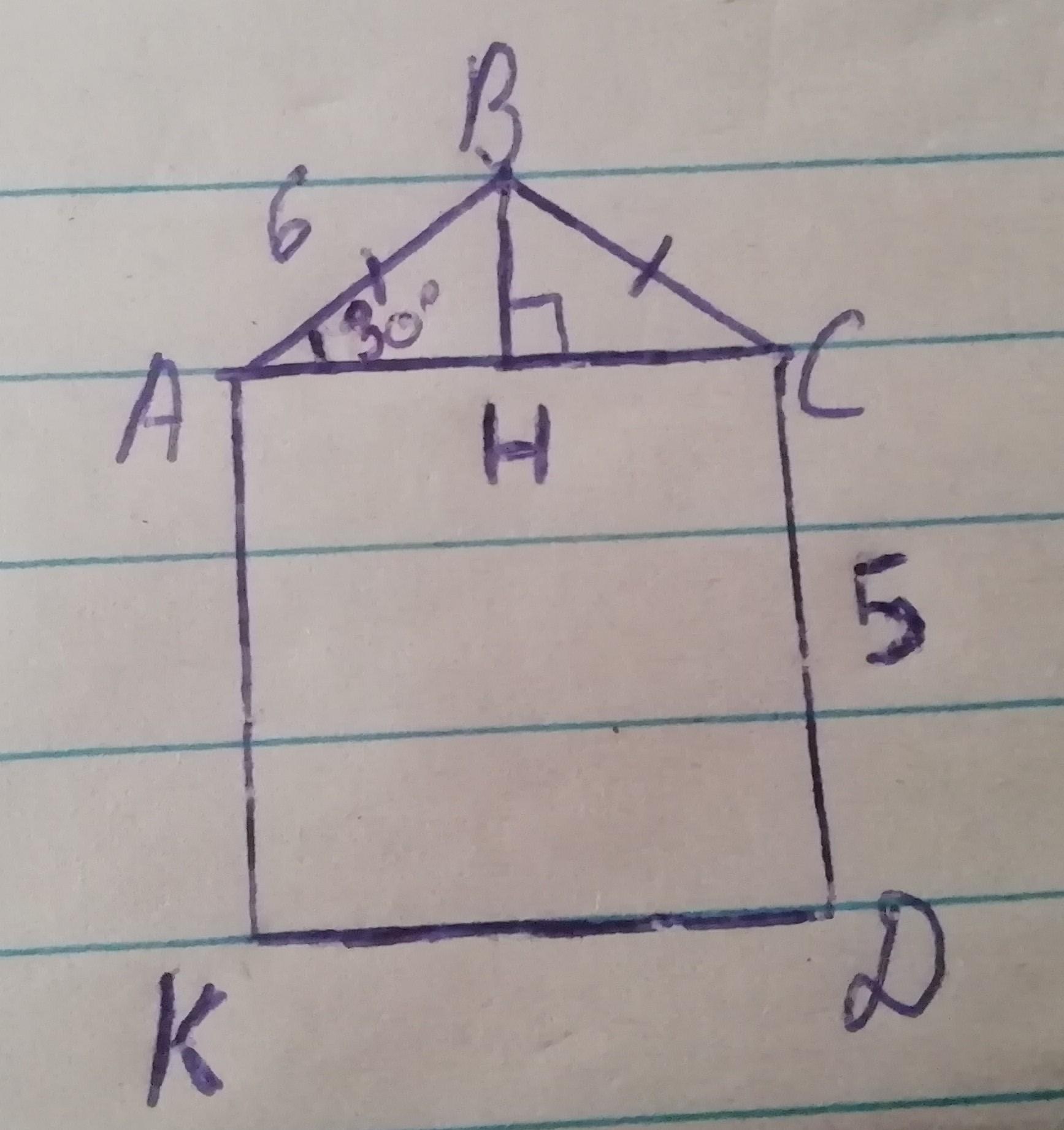
Рассмотрим ΔABC
AB = BC = 6 м ==> ΔABC равнобедренный.
Построим BH перпендикулярно AC
В прямоугольном треугольнике высота, проведённая к основанию, является его биссектрисой (делит угол на 2 равных угла)
==> ∠ABH = ∠ABC/2 = 120/2 = 60°
Рассмотрим ΔABH: AB = 6 м, ∠ABH = 60°, ∠H - прямой.
∠A = 90 - 60 = 30° (сумма острых углов прямоугольного треугольника равна 90°)
BH = AB/2 = 6/2 = 3 м (в прямоугольном треугольнике катет, лежащий напротив угла в 30°, равен половине гипотенузы)
Пусть высота дома равна h
h = BH + CD = 3 + 5 = 8 м
Ответ: h = 8 м.
AB = BC = 6 м ==> ΔABC равнобедренный.
Построим BH перпендикулярно AC
В прямоугольном треугольнике высота, проведённая к основанию, является его биссектрисой (делит угол на 2 равных угла)
==> ∠ABH = ∠ABC/2 = 120/2 = 60°
Рассмотрим ΔABH: AB = 6 м, ∠ABH = 60°, ∠H - прямой.
∠A = 90 - 60 = 30° (сумма острых углов прямоугольного треугольника равна 90°)
BH = AB/2 = 6/2 = 3 м (в прямоугольном треугольнике катет, лежащий напротив угла в 30°, равен половине гипотенузы)
Пусть высота дома равна h
h = BH + CD = 3 + 5 = 8 м
Ответ: h = 8 м.
Приложения:
Ответил ClarisVerbis
0
Добрый вечер! Подскажите, пожалуйста https://znanija.com/task/31897602
Новые вопросы
Русский язык,
1 год назад
Английский язык,
1 год назад
Химия,
7 лет назад
Математика,
7 лет назад
Алгебра,
8 лет назад