Найдите вторую производную, точки перегиба и определите характер выпуклости: у=(x^2+2x+4)/(x+2)
Ответы на вопрос
Ответил xxxeol
0
ДАНО
Y=(x^2 + 2x + 4)/(x + 2)
ИССЛЕДОВАНИЕ
1. Область определения - Х≠ -2.
Х∈(-∞;-2)∪(-2;+∞)
2. Пересечение с осью Х - нет. Х∈∅.
3. Пересечение с осью У.
Y(0) =2.
4. Наклонная асимптота - Y = x
5 Проверка на чётность.
Y(-x) ≠ Y(x).
Функция ни четная ни нечетная.
6. Поведение в точке разрыва.
lim(->-2) Y(x) = -∞.
lim(-2<-) Y(x) = +∞
5, Первая производная.

6. Локальные экстремумы.
Y'(x) = 0
x= -4 - локальный максимум. - Y(-4) = -6
х = 0 - локальный минимум Y(0) = 2
7. Участки монотонности функции.
Возрастает - при Y'(X) >0 - Х∈(-∞;-4]∪[0;+∞)
Убывает - при Y'(x) <0 - X∈[-4;-2)∪(-2;0]
8. Вторая производная - поиск точки перегиба

Точки перегиба нет. У функции две отдельные ветви с разрывом при Х = -2.
9. Выпуклая - "горка" - Y"(x)<0 при Х∈(-∞;-2)
Вогнутая - "ложка" - Y"(x)>0 при Х∈(-2;+∞)
10. Поведение на бесконечности
Y(-∞) = - ∞ и Y(+∞) = + ∞
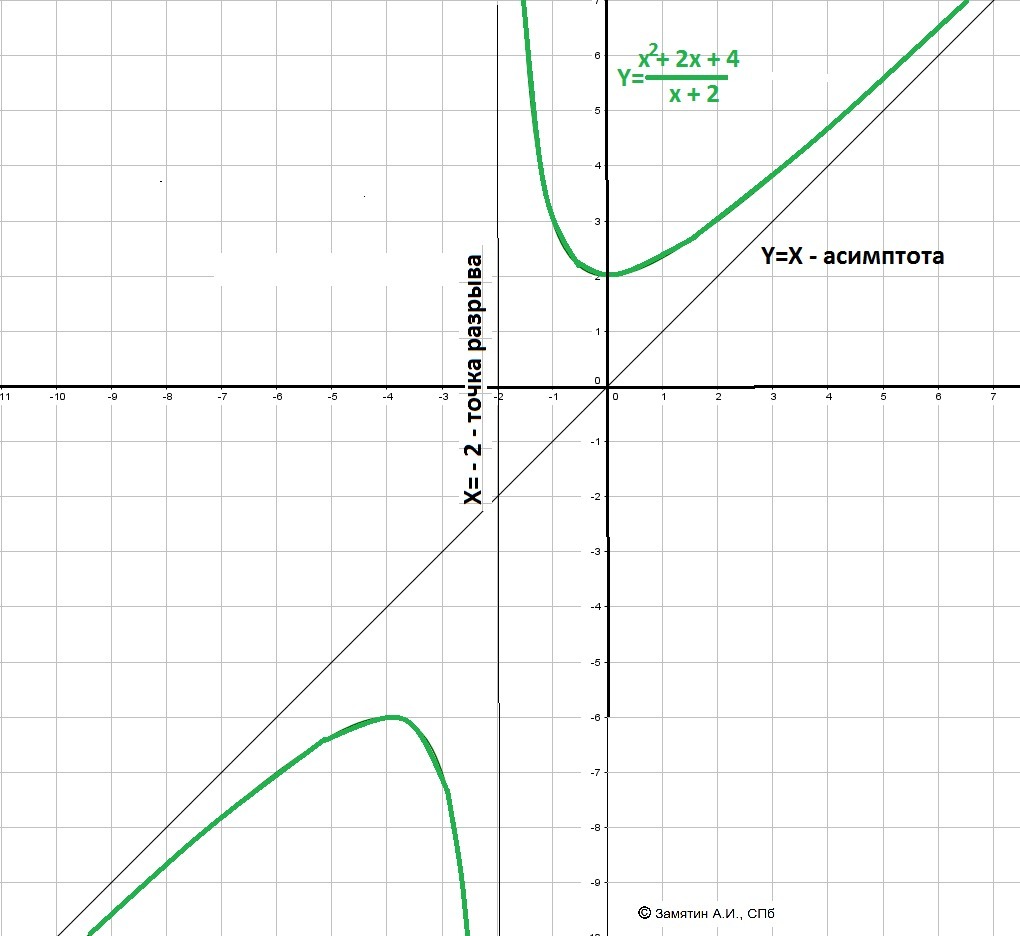
10. График в приложении.
Y=(x^2 + 2x + 4)/(x + 2)
ИССЛЕДОВАНИЕ
1. Область определения - Х≠ -2.
Х∈(-∞;-2)∪(-2;+∞)
2. Пересечение с осью Х - нет. Х∈∅.
3. Пересечение с осью У.
Y(0) =2.
4. Наклонная асимптота - Y = x
5 Проверка на чётность.
Y(-x) ≠ Y(x).
Функция ни четная ни нечетная.
6. Поведение в точке разрыва.
lim(->-2) Y(x) = -∞.
lim(-2<-) Y(x) = +∞
5, Первая производная.
6. Локальные экстремумы.
Y'(x) = 0
x= -4 - локальный максимум. - Y(-4) = -6
х = 0 - локальный минимум Y(0) = 2
7. Участки монотонности функции.
Возрастает - при Y'(X) >0 - Х∈(-∞;-4]∪[0;+∞)
Убывает - при Y'(x) <0 - X∈[-4;-2)∪(-2;0]
8. Вторая производная - поиск точки перегиба
Точки перегиба нет. У функции две отдельные ветви с разрывом при Х = -2.
9. Выпуклая - "горка" - Y"(x)<0 при Х∈(-∞;-2)
Вогнутая - "ложка" - Y"(x)>0 при Х∈(-2;+∞)
10. Поведение на бесконечности
Y(-∞) = - ∞ и Y(+∞) = + ∞
10. График в приложении.
Приложения:
Новые вопросы