Найдите угол наклона кривой в заданной точке.
Приложения:
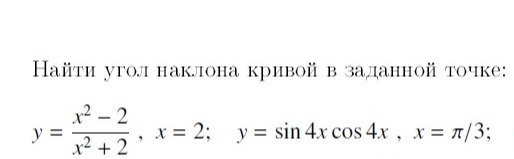
Ответы на вопрос
Ответил sedinalana
1
tga=f`(x0)
1
f`(x)=(2x³+4x-2x³+4x)/(x²+2)²=8x/9x²+2)²
f`(2)=16/36=4/9
tga=4/9
a=arctg4/9
2
y=1/2*sin8x
f`(x)=1/2*cos8x*8=4cos8x
f`(π/3)=4cos(8π/3)=4cos(2π+2π/3)=4cos(π-π/3)=-4cosπ/3=-4*1/2=-2
tga=-2
a=π-arctg2
1
f`(x)=(2x³+4x-2x³+4x)/(x²+2)²=8x/9x²+2)²
f`(2)=16/36=4/9
tga=4/9
a=arctg4/9
2
y=1/2*sin8x
f`(x)=1/2*cos8x*8=4cos8x
f`(π/3)=4cos(8π/3)=4cos(2π+2π/3)=4cos(π-π/3)=-4cosπ/3=-4*1/2=-2
tga=-2
a=π-arctg2
Ответил ПрофиЗнания
0
tgx=y'
y'=(x²-2)'(x²+2)-(x²-2)(x²+2)' / (x²+2)² = 2x(x²+2)-2x(x²-2)/(x²+2)²=
=2x³+4x-2x³+4x/(x²+2)² = 8x/(x²+2)² = 8*2/(2²+2)²=16/36 =4/9
tgx=4/9
x=arctg 4/9
_______________________________________________________
y=sin4xcos4x=1/2 sin8x
y'=1/2 *cos8x * 8=4cos8x=4cos 8π/3 = 4cos (2π+2π/3)= - 2 четверть ,cos отриц.
=-4cos π/3 = -4*1/2=-2
tgx=-2
x=-arctg2+πn , n∈Z
y'=(x²-2)'(x²+2)-(x²-2)(x²+2)' / (x²+2)² = 2x(x²+2)-2x(x²-2)/(x²+2)²=
=2x³+4x-2x³+4x/(x²+2)² = 8x/(x²+2)² = 8*2/(2²+2)²=16/36 =4/9
tgx=4/9
x=arctg 4/9
_______________________________________________________
y=sin4xcos4x=1/2 sin8x
y'=1/2 *cos8x * 8=4cos8x=4cos 8π/3 = 4cos (2π+2π/3)= - 2 четверть ,cos отриц.
=-4cos π/3 = -4*1/2=-2
tgx=-2
x=-arctg2+πn , n∈Z
Новые вопросы