Найдите угол между УГОЛ между касательными, касательными, проведенными ИЗ ТОЧКИ, внешней по отношению к окружности, если точки касания делят Окружность на две дуги, относящиеся как: 3:15
Ответы на вопрос
Ответил bertramjeratire
9
Ответ:
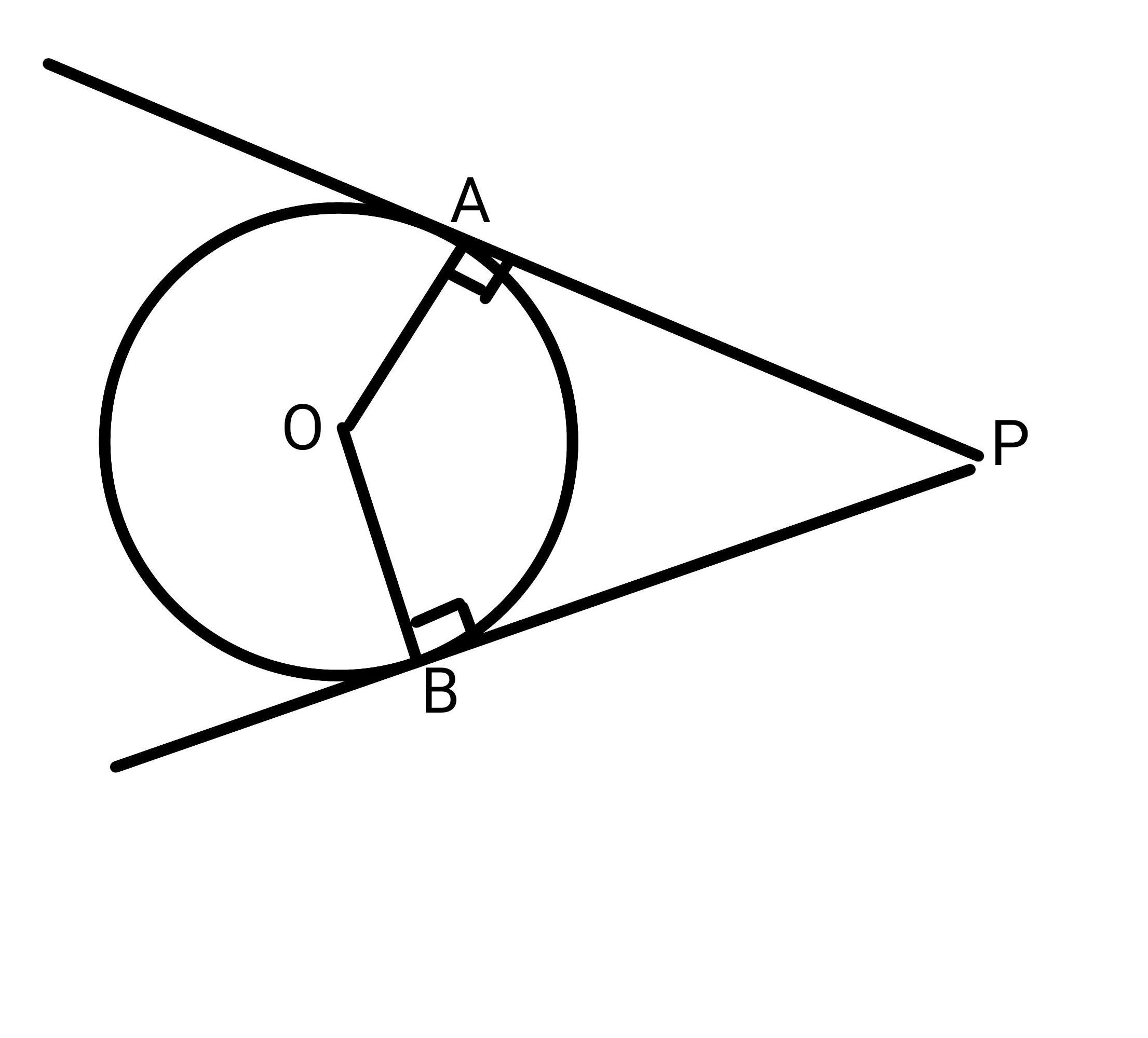
Касательная к окружности и радиус, проведенный в точку касания, взаимно перпендикулярны, поэтому углы ∠PBO=∠PAO=90°
Найдем меньший угол AOB=3x, а больший 15x.
Общий угол окружности 360°.
Нам нужен меньший 3x.
3x=3×20°=60°.
PAOB – четырехугольник, сумма внутренних углов четырехугольника 360°.
∠PAO+∠AOB+∠OBP+∠APB=360°
90°+60°+90°+∠APB=360°
240°+∠APB=360°
∠APB=360°-240°
∠APB=120°
∠APB – это и есть нужный нам угол между касательными.
Приложения:
Новые вопросы
Русский язык,
1 год назад
Русский язык,
1 год назад
Алгебра,
6 лет назад
Математика,
8 лет назад
Физика,
8 лет назад