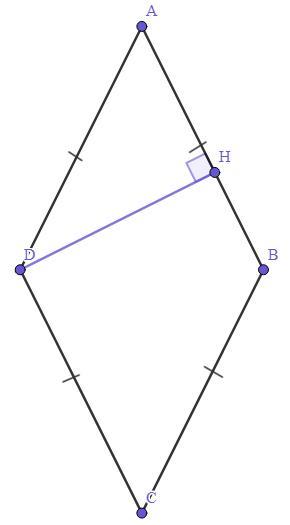
Найдите углы ромба, если его периметр равен 24 см, а высота - 3 см
Ответы на вопрос
Ответ:
1)периметр ромба АВСД равен АВ+АД+ДС+ВС=24 см, т.к. у ромба все стороны равны,из этого следует что ВА=АД=ДС=ВС= 24:4= 6см
2)если в прямоугольном треугольнике (ВАО, при ВО- перпендикуляре к АД) катед (ВО равен 3см) в два раза меньше гипотенузы (ВА равной 6 см) то этот катед лежит на против угла равного 30' (угол ВАО равен 30 градусов)
3)Проведем диогональ ромба АС
4)Диогональ ромба является биссектрисой обойх внутренних углов ромба,через которые она проходит, из этого следует что угол ВАС =угол САД=30 градусов :2= 15 градусов и равен углу ВСА и углу АСД
5)треугольник ВАС: угол АВС +угол ВАС+ угол АСБ = 180 градусов, из этого следует что угол АВС=180градусов -(15+15)=150 градусов.
Дано :
Четырёхугольник ABCD - ромб.
Р(ABCD) = 24 см.
DH - высота, DH = 3 см.
Найти :
∠A = ? ; ∠В = ? ; ∠С = ? ; ∠D = ?
Решение :
- Ромб - это параллелограмм, все стороны которого равны между собой.
Отсюда AD = Р(ABCD) : 4 = 24 см : 4 = 6 см.
Рассмотрим ΔADH - прямоугольный (так как ∠AHD = 90°).
Заметим, что 0,5*AD = DH (0,5*6 см = 3 см).
- Если в прямоугольном треугольнике катет равен половине гипотенузы, то напротив этого катета лежит угол, равный 30°.
Отсюда ∠А = 30°.
- В ромбе сумма соседних углов равна 180°.
Следовательно -
∠А + ∠В = 180°
∠В = 180° - ∠А = 180° - 30° = 150°.
- В ромбе противоположные углы равны.
Отсюда -
∠A = ∠C = 30°
∠B = ∠D = 150°.
Ответ :
30° ; 150° ; 30° ; 150°.