Математика, вопрос задал Davish , 9 лет назад

Найдите точки экстремума функции: y=x*sqrt(8-x^(2)).

Ответы на вопрос

Ответил Nastya808080

0

$y=x* sqrt{8- x^{2}}$
y'= $sqrt{8- x^{2}}+ frac{x*(-2x)}{ sqrt{8- x^{2}}} = frac{8- x^{2} -2 x^{2} }{ sqrt{8- x^{2}}} =$ $frac{8-3 x^{2} }{sqrt{8- x^{2}}}$
y'=0 => $frac{8-3 x^{2} }{sqrt{8- x^{2}}}=0 => 8-3 x^{2} =0=> x^{2} = frac{8}{3} => x1= frac{2 sqrt{2} }{ sqrt{3} } = frac{2 sqrt{6} }{3} ; x2=- frac{2 sqrt{6} }{3}$
Но: $8- x^{2}>0 => x^{2} <8 =>$ x∈ $(-2 sqrt{2} ;2 sqrt{2})$
При $-2 sqrt{2} < x leq frac{-2 sqrt{6} }{3}; y<0$ (при х=-2 у=-2)
При $frac{-2 sqrt{6} }{3}<span>0$ (при х=0 у=2 $sqrt{2}$ )
При $frac{2 sqrt{6} }{3} < x leq 2 sqrt{2}; y<0$ (при х=2 у=-2)
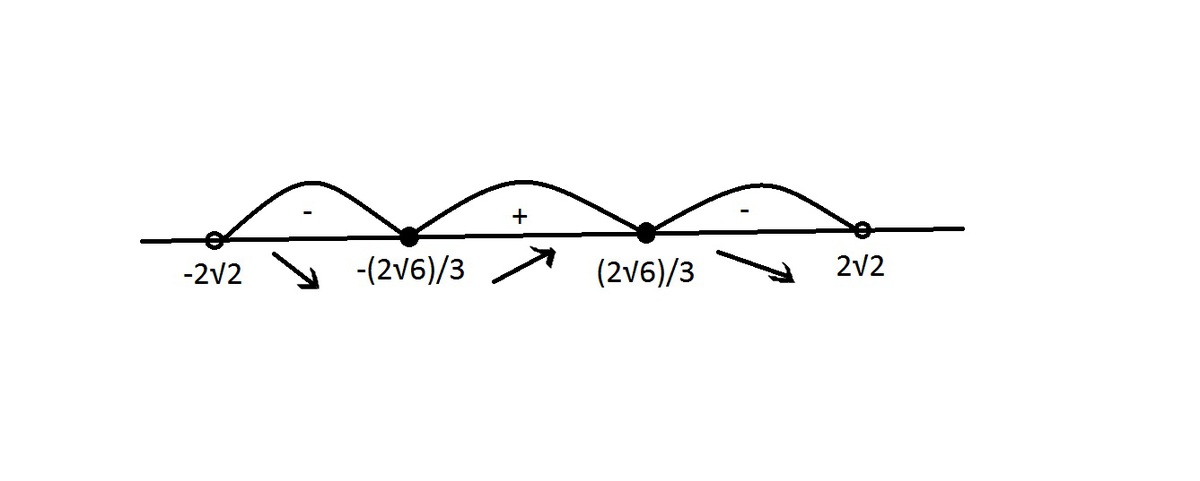
На промежутках, в которых производная функции >0 функция возрастает, где <0 - убывает =>
точки экстремума: $frac{-2 sqrt{6} }{3}$ и $frac{2 sqrt{6} }{3}$

Приложения:

Ответил Davish

0

Спасибки :*

Ответил Davish

0

Большое^^

Ответил Davish

0

Решите неравенство: x-2/log{0,3}5}> 0

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Информатика, 2 года назад

Определите синтаксическую ошибку программного кода ...

Математика, 2 года назад

решите уравнение x + 2/3 - = 2x + 1/9 - x / 3...

Математика, 9 лет назад

В коробке имеются конфеты четырёх сортов. Какое наименьшее число конфет надо взять наугад, не заглядывая в коробку, чтобы среди вынутых конфет оказались хотя бы 2 конфеты одного сорта?

История, 9 лет назад

какие жанры были характерны для русской литературы XVII в?

История, 9 лет назад

единое еврейское государство образовалось ...

Алгебра, 9 лет назад

Авиабилет для взрослого стоит 4000 рублей. Стоимость билета для школьников составляет 65% от стоимости билета для взрослого. Группа состоит из 13 школьников и 6 взрослых. Сколько рублей стоят билеты...