Математика, вопрос задал egorka7248 , 7 лет назад

Найдите точки экстремума функции
u (x, y)

Приложения:

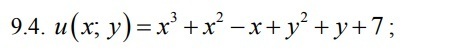
Ответы на вопрос

Ответил Liamus

для нахождения точек экстремума функции нужно решить систему уравнений:

$begin{cases}frac{partial u}{partial x}=0,\frac{partial u}{partial y}=0;end{cases}$

где $frac{partial u}{partial }$ - соответствующие частне производные. Получим:

$begin{cases}3x^2+2x-1=0,\2y+1=0;end{cases}Rightarrow begin{cases}x_1=-1,,x_2=frac{1}{3},\y=-frac{1}{2}.end{cases}$

то есть имеем 2 критические точки $Aleft(-1;-frac{1}{2}right),,Bleft(frac{1}{3};-frac{1}{2}right)$

Поскольку в точке А:

$frac{partial^2u}{partial x^2}cdotfrac{partial^2u}{partial y^2}-(leftfrac{partial^2u}{partial xpartial y}right)^2=-4cdot 2-0=-8<0$

то в этой точке нет экстремума функции

а в точке B:

$frac{partial^2u}{partial x^2}cdotfrac{partial^2u}{partial y^2}-(leftfrac{partial^2u}{partial xpartial y}right)^2=4cdot 2-0=8>0$

есть экстремум.

Ответ: $Bleft(frac{1}{3};-frac{1}{2}right)$ - единственная точка экстремума.

Новые вопросы

Математика, 1 год назад

Английский язык, 1 год назад

Физика, 7 лет назад

Геометрия, 7 лет назад

Алгебра, 8 лет назад

Литература, 8 лет назад