найдите точки экстремума функции
Приложения:
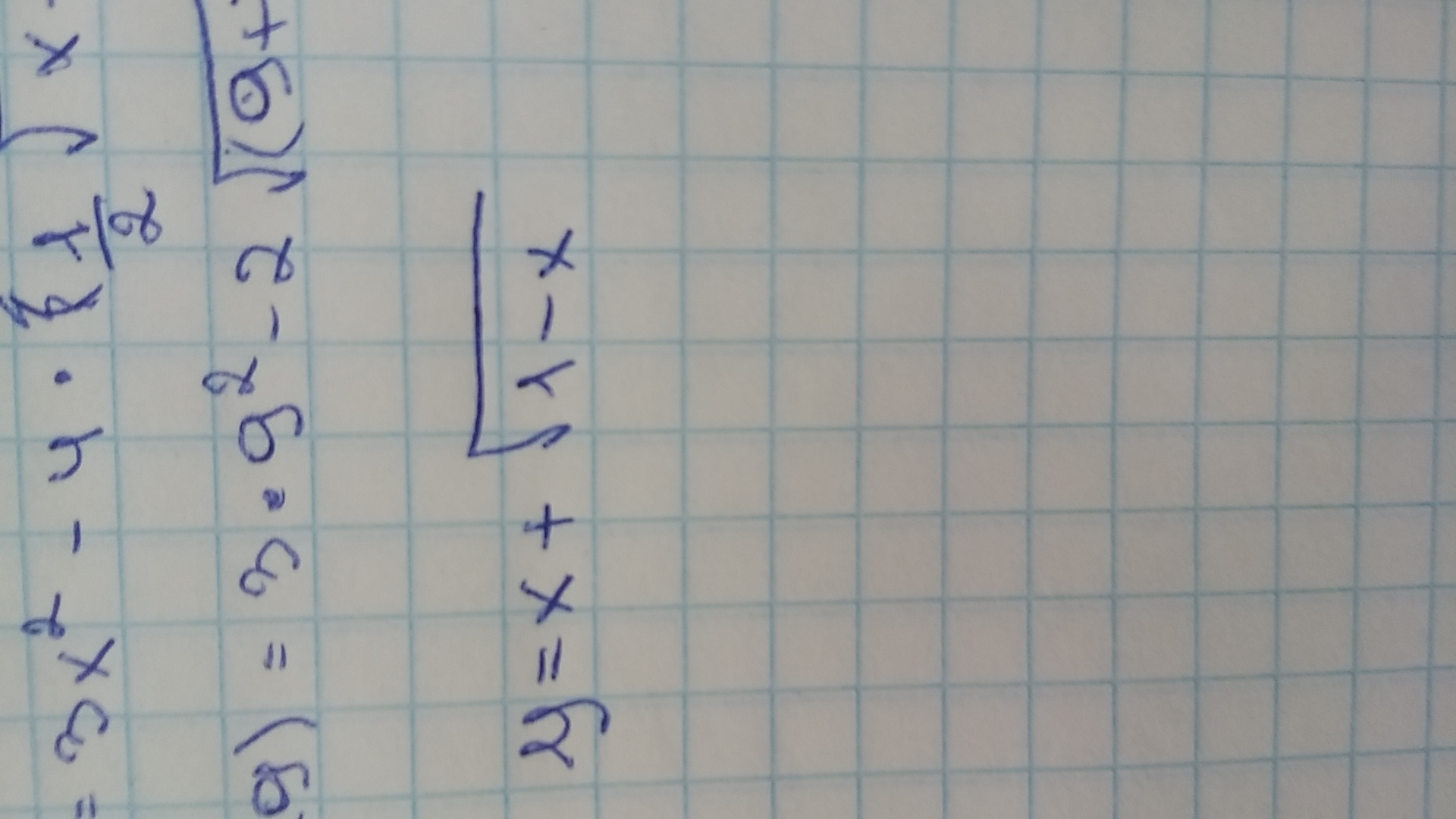
Ответы на вопрос
Ответил Minsk00
0
Найти точки экстремума функции 
Решение:Область определения функции 1-х≥0 или х≤1
Найдем производную функции


Найдем критические точки приравняв производную к нулю




На числовой прямой отобразим эту точку и найдем методом подстановки знаки производной.
Например при х=0 производная y'=1-1/2=0,5>0
+ 0 -
------------!----------!
3/4 1
Следовательно в точке х=3/4=0,75 функция имеет максимум
Решение:Область определения функции 1-х≥0 или х≤1
Найдем производную функции
Найдем критические точки приравняв производную к нулю
На числовой прямой отобразим эту точку и найдем методом подстановки знаки производной.
Например при х=0 производная y'=1-1/2=0,5>0
+ 0 -
------------!----------!
3/4 1
Следовательно в точке х=3/4=0,75 функция имеет максимум
Ответил Sandria11
0
много скобок и тд не могу понять решение
Ответил Minsk00
0
Скобки только при нахождении производной как степени. Если применить табличную формулу нахождения производной квадратного корня то останется одни скобки.
Ответил Minsk00
0
При нахождении производной первоначально рассматриваем производную суммы. Поэтому раскрыв первые скобки мы имеет сумму производных х и (1-х) в степени 0,5. Далее производная степенной функции 1-х котороя равна самой степени (1/2) умноженной на функцию со степенью (1/2-1) и умноженной на производную (1-х)'= 1'-x'=-1
Новые вопросы