Найдите сумму квадратов корней уравнения
Приложения:
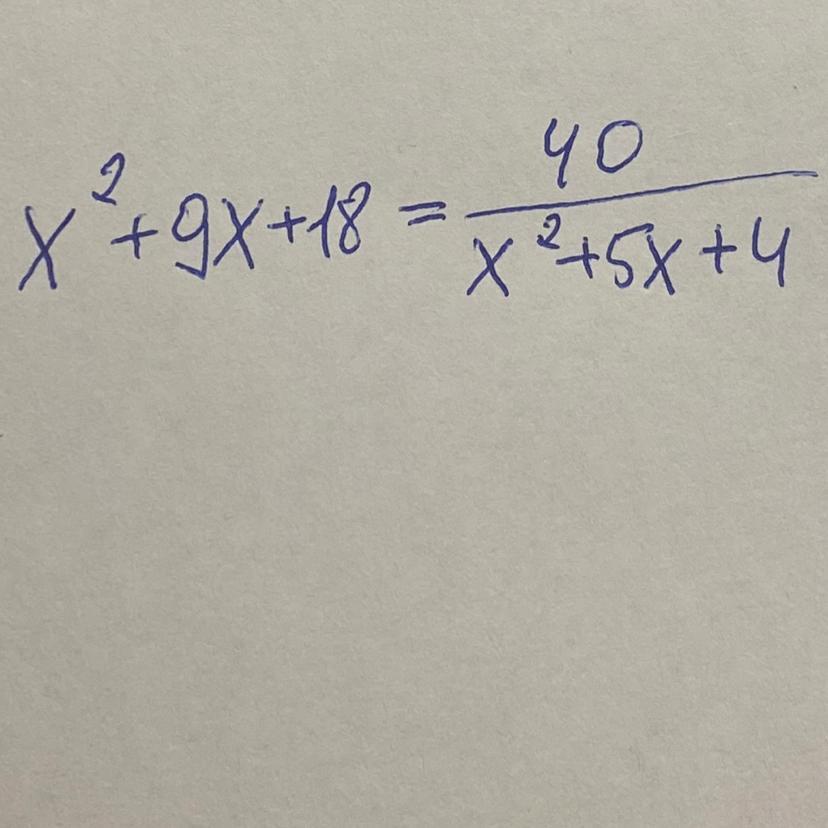
Ответы на вопрос
Ответил balakine977
1
Ответ:
62
Пошаговое объяснение:
Если x ≠ -1 и x ≠ -4, то данное уравнение можно записать так:
(умножить обе части на знаменатель правой части и раскрыть скобки, перенести 40 влево). x= -1 и x = -4 - не являются корнями, значит переход равносилен.
Пусть корни данного уравнения это a, b, c, d. Тогда его можно записать в виде:
Раскрывая скобки, получаем:
Это тот же самый многочлен, но записанный с помощью a, b, c и d. Значит его коэффициенты равны, то есть a + b + c + d = 14, ab+ac+bc+bd+ab+cd = 67
Чтобы получить сумму квадратов, возведём обе части первого равенства в квадрат:
Раскрывая скобки, получаем:
, откуда
ab+ac+bc+bd+ab+cd = 67, значит
sankovsky85:
К сожалению, ваше решение не оказалось правильным
Я решил. У меня получилось 45
Получается так:
Сначала раскладываем эти квадратные уравнения
После введённого ОДЗ что x не может быть равен -1 и -4 можно записать это так:
(x+3)(x+6)(x+1)(x+4)=40
После этого я попробовал найти что-то схожее я перемножил первую скобку с последней и вторую с третьей
Сначала раскладываем эти квадратные уравнения
После введённого ОДЗ что x не может быть равен -1 и -4 можно записать это так:
(x+3)(x+6)(x+1)(x+4)=40
После этого я попробовал найти что-то схожее я перемножил первую скобку с последней и вторую с третьей
Получилось (x^2+7x+12)(x^2+7x+6)=40
x^+7x заменил на t
t получилось равным:
t = -2
t = -16
Проставил обратно
-16 в пролёте, так как дискриминант меньше нуля
Значит -2
получилось: x^2+7x+2=0
x1+x2=-7
x1*x2=2
Дальше по формуле:
a^2+b^2=(a+b)^2-2ab=49-4=45
Ответ: 45
x^+7x заменил на t
t получилось равным:
t = -2
t = -16
Проставил обратно
-16 в пролёте, так как дискриминант меньше нуля
Значит -2
получилось: x^2+7x+2=0
x1+x2=-7
x1*x2=2
Дальше по формуле:
a^2+b^2=(a+b)^2-2ab=49-4=45
Ответ: 45
Если учитывать только действительные корни, то вы правы. В общем виде ответ 62 (можете проверить, например с помощью wolfram alpha)
Новые вопросы