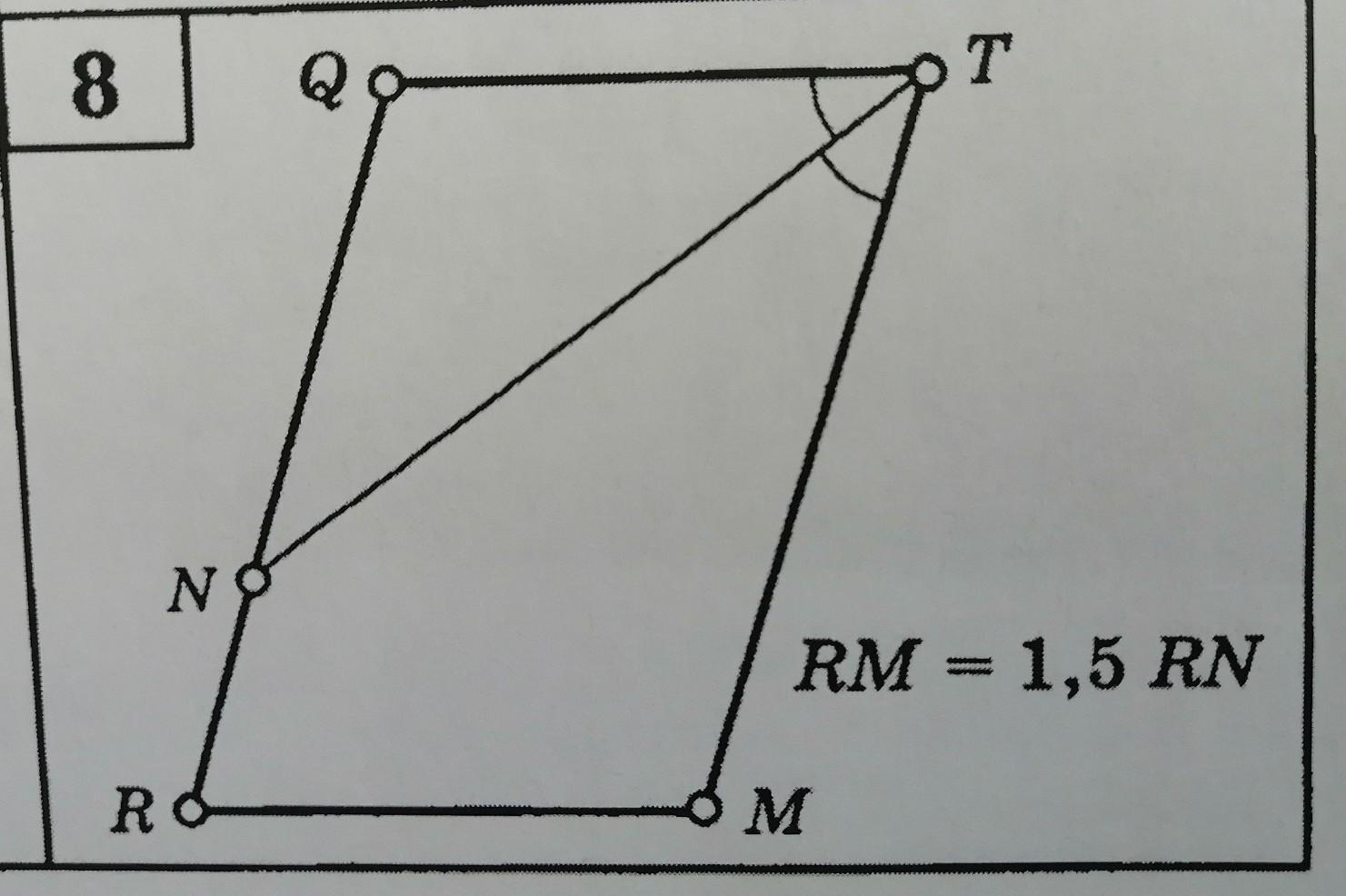
Найдите стороны параллелограмма, если (периметр) P=36.
Помогите пожалуйста. Срочно!
Приложения:
ВикаБач:
RN=x; RM=1.5x; QR=RN+QN=x+1.5x=2.5x; P=2(RM+QR)=2(1.5x+2.5x)=8x=36; x=4.5; RM=1.5x=1.5*4.5=6.75; QR=2.5x=2.5*4.5=11.25;
Четырехугольник, случайно, не параллелограмм?
Да, параллелограмм
Ответы на вопрос
Ответил Andr1806
1
Ответ:
Стороны параллелограмма равны
RM = QT =6,75 ед. RQ = MT = 11,25 ед.
Объяснение:
ЕСЛИ четырехугольник - параллелограмм, то
QT = RM как противоположные стороны параллелограмма. Проведем NP параллельно RM. Тогда треугольники NQT и NPT равны по двум сторонам (QT=NP, NT - общая) и углу между ними. (NT - биссектриса и ∠QTN = ∠PTN).
∠TNР = ∠QTN - внутренние накрест лежащие при параллельных QT и NP и секущей NT. Отсюда ΔNQT равнобедренный и QN = QT = RM.
А вот теперь доказано, что
RQ = RN+QN = RN+RM = 2,5RN.
Тогда периметр равен
P = 2·(RQ+RM) = 2·(2,5RN+1,5RN) = 8·RN.
Следовательно, 36 = 8·RN и RN = 4,5 ед.
Тогда RM = 6,75 ед, а RQ = 11,25 ед.
Приложения:

Новые вопросы