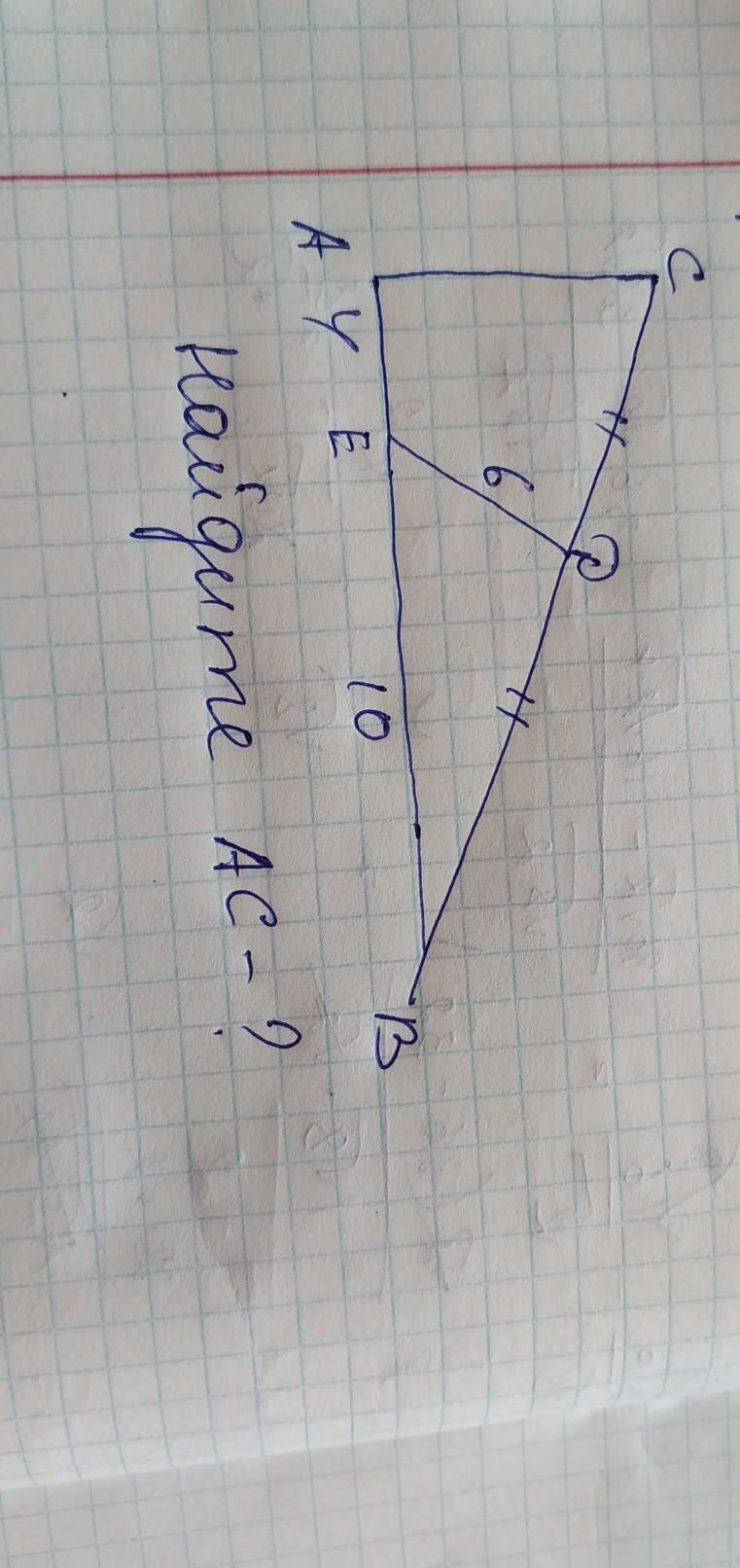
найдите сторону треугольника с объяснением угол А прямоугольный
Приложения:
guseinramazanov:
да ,он прямоугольный
да , все , угол А прямоугольный
10-11 кл
Самый примитивный способ - теорема косинусов для треугольника EDB, где DB = х. Тогда х^2 + 10^2 - 2x*10*14/2x = 36, откуда х = 2 корня из 19. Тогда квадрат гипотенузы ВС равен 16*19 = 304, а искомый отрезок АС (по теореме Пифагора) 6 корней из 3.
Через отношение сторон в прямоугольном треугольнике АВС.
Ответы на вопрос
Ответил marktopskiy34567
0
Дано:
ΔABC - прямоугольный (∠A = 90°)
AB = 14
AE = 4
EB = 10
ED = 6
(•) D - середина гипотенузы (BC)
Найти:
AC
Решение:
• Пусть половина гипотенузы (BC) = x, т.е.:
CD = DB = x
• Рассмотрим ΔEDB, по теореме косинусов:
ED² = EB² + DB² - 2 • EB • DB • cos∠CBD
( cos∠CBD = AB/CB = 14/2x )
6² = 10² + x² - 2 • 10 • x • 14/2x
36 = 100 + x² - 20x • 14/2x
36 = 100 + x² - 140
x² - 76 = 0
x² = 76
x = √76
x = √(4 • 19)
x = 2√19
• Находим гипотенузу:
BC = 2 • x = 2 • 2√19 = 4√19
• В прямоугольном треугольнике ABC по теореме Пифагора:
BC² = AB² + AC², ⇒ AC = √(BC² - AB²)
AC = √((4√19)² - 14²) = √(304 - 196) = √108 = 6√3
Ответ: AC = 6√3
Новые вопросы