Алгебра, вопрос задал kzkzkz20030511 , 1 год назад

Найдите решение уравнения на указанном интервале:
sin5x-cos4x=0 360°

cos6x-sin3x=0 90°

kzkzkz20030511: 360 меньше Х меньше 450

kzkzkz20030511: первое

kzkzkz20030511: да

kzkzkz20030511: 90 меньше Х меньше 180

kzkzkz20030511: строго меньше

kzkzkz20030511: спасиб :)

Ответы на вопрос

Ответил igundane

28

$1)sin(5x)-cos(4x)=0<=>sin(5x)-sin(\frac{\pi}{2}-4x )=0<=>\\<=>cos(\frac{2x+\pi}{4} )sin(\frac{18x-\pi}{4} )=0\\cos(\frac{2x+\pi}{4} )=0=>x=\frac{\pi}{2}+2\pi k\\ sin(\frac{18x-\pi}{4} )=0<=>18x-\pi=4\pi k<=>x=\frac{\pi}{18}+\frac{2\pi k}{9}\\x=\frac{\pi}{18}+\frac{2\pi k}{9}$

$2)cos(6x)-sin(3x)=0<=>sin(\frac{\pi}{2}-6x )-sin(3x)=0<=>\\<=>cos(\frac{\pi-6x}{4} )sin(\frac{\pi-18x}{4} )=0\\cos(\frac{\pi-6x}{4} )=0=>x=\frac{\pi}{2}+\frac{2\pi k}{3}\\ sin(\frac{\pi-18x}{4} )=0=>x=\frac{\pi}{18}+\frac{2\pi k}{9}\\x=\frac{\pi}{18}+\frac{2\pi k}{9}$

Приложения:

Предыдущий вопрос

Следующий вопрос

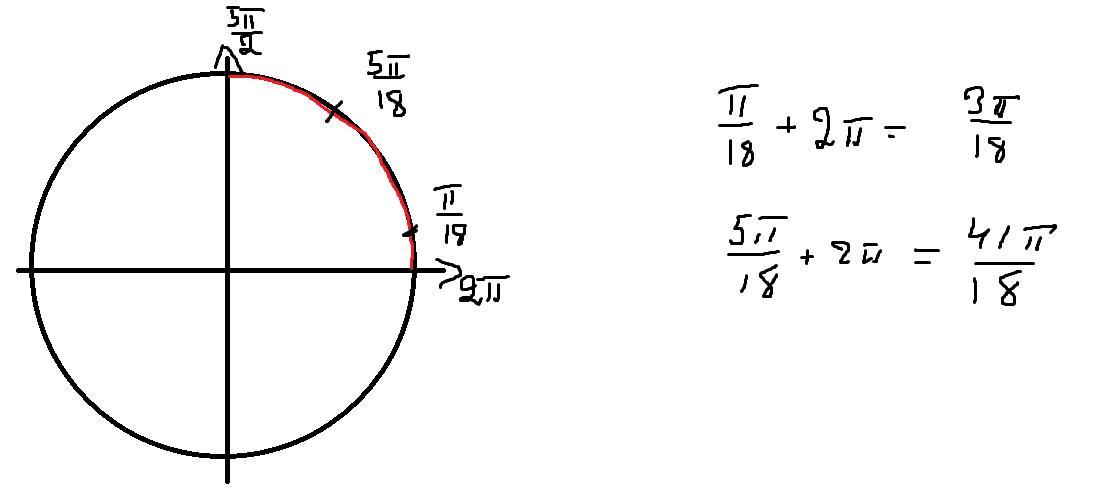
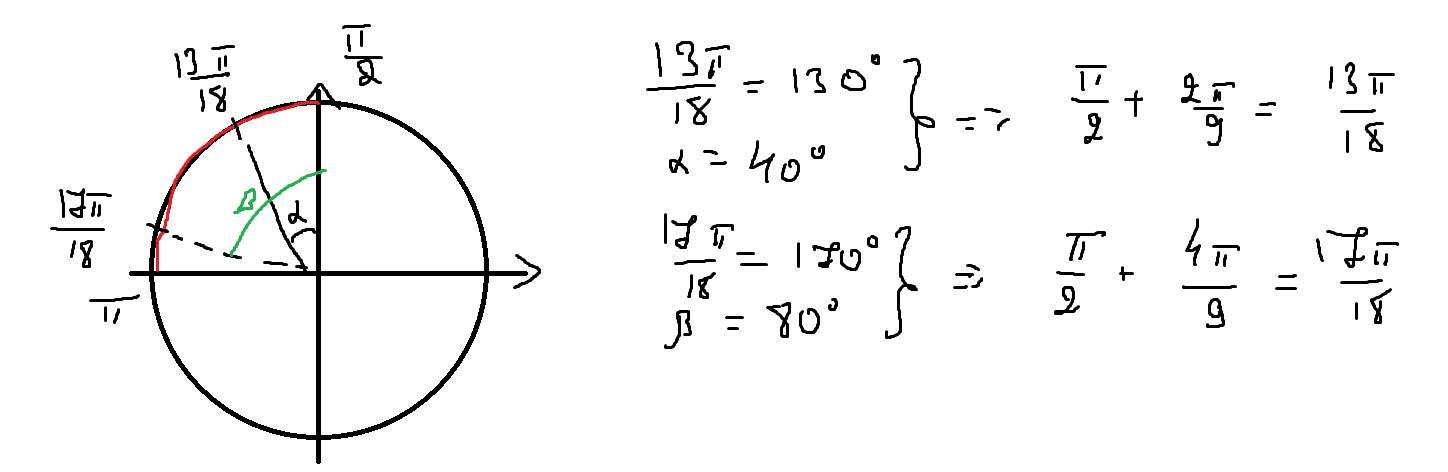
Новые вопросы

Информатика, 1 год назад

дз по информатике: рассказать о проблемах информационного мира...

Английский язык, 1 год назад

Look at the words in bold. Write new words with un-, im- or in-. That woman is horrible. She's really friendly. unfriendly 1 This map of my hometown isn't correct. It's very accurate....... 2...

Математика, 1 год назад

Помогите пожалуйста решить с обьяснением. В магазин привезли 215кг яблок,113кг апельсинов,182кг мандаринов и 197кг груш.За неделю все фрукты раскупили,причём каждый день их продавалось одинаковое...

Математика, 1 год назад

помогите пожалуйста 13/4+(-1/2)...

Химия, 6 лет назад

вычислить массовую долю элемента Ca2So4...

Русский язык, 6 лет назад

63 упр . Из 4 абзаца нужно выписать все словосочетания и написать их связь (примык , согл , управлен) и показать стрелочкойт главное слово . И если не сложно вопрос и часть речи подписать...