Алгебра, вопрос задал dream2016 , 7 лет назад

Найдите произвольную функции y=ctg(ln((e^x+e^-x)/x)) Срочно!

Приложения:

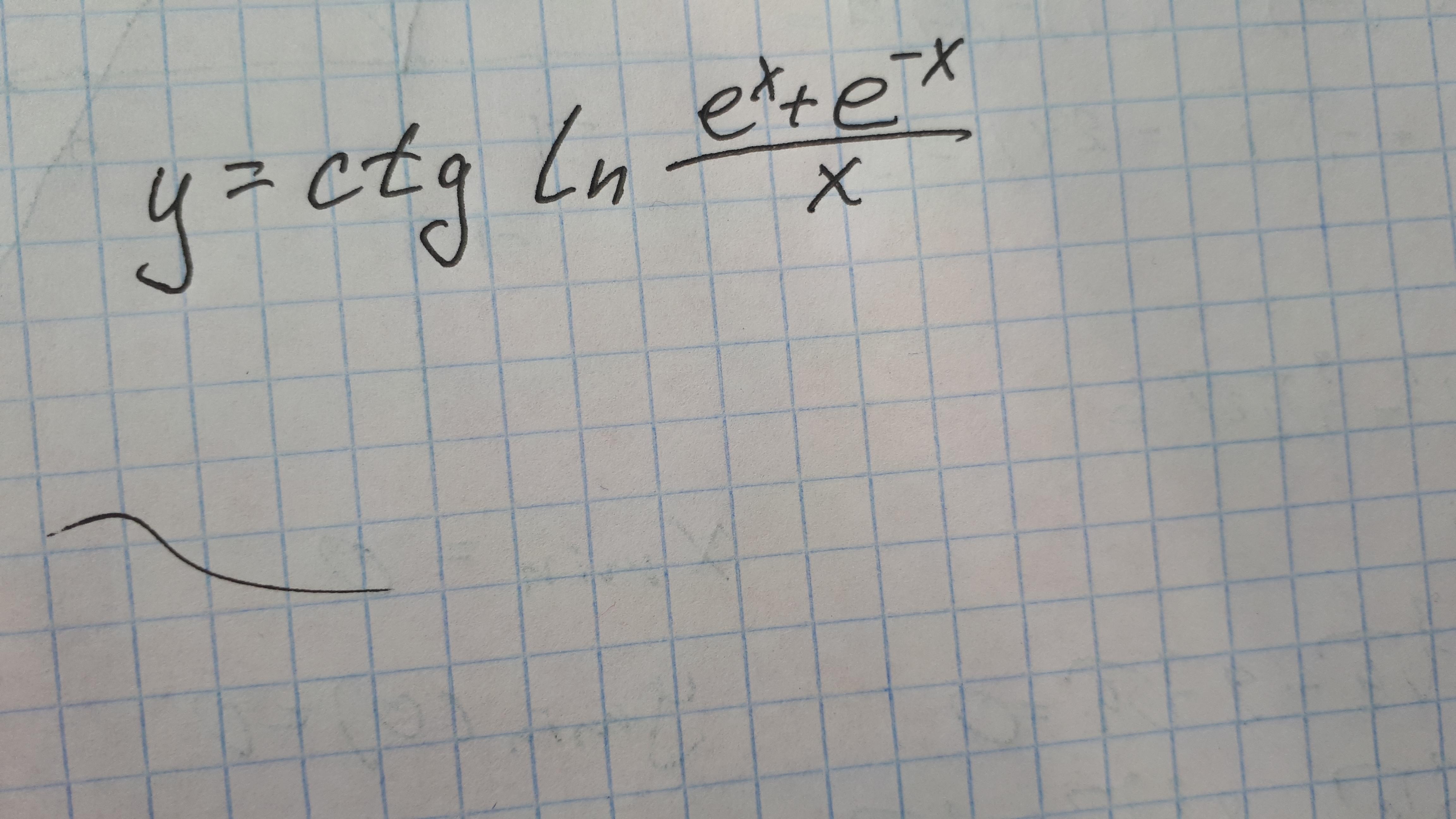
Ответы на вопрос

Ответил natalyabryukhova

Ответ:

$y=ctg lnfrac{e^x+e^-^x}{x}\ \y'=-frac{1}{sin^2lnfrac{e^x+e^-^x}{x}}*frac{1}{frac{e^x+e^-^x}{x}}*frac{(e^x+e^-^x*(-1))*x-(e^x+e^-^x)}{x^2}=-frac{1}{sin^2lnfrac{e^x+e^-^x}{x}}*frac{x}{e^x+e^-^x}* frac{(e^x-e^-^x)*x-(e^x+e^-^x)}{x^2}$

Объяснение:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

Аргументы в сочинении на тему возраста...

Русский язык, 1 год назад

"Уцепилась" слово по составу...

География, 7 лет назад

Вот идет Гиппопотам. Он идет от Занзибара, Он идет к Килиманджаро... Почему Гиппопотам не может идти от Занзибара к Килиманджаро? 1) Гиппопотам, на самом деле, умеет только плавать...

Химия, 7 лет назад

Установите соответствие: Реагенты: 1. купрум (II) хлорид и калий гидроксид 2. аргентум нитрат и натрий фосфат 3. кальций карбонат и хлоридная кислота 4. кальций сульфит и бромидная кислота...

Математика, 8 лет назад

Найдите все делители чисел и их общие делители,1) 40и60;2)60и75.

Математика, 8 лет назад

Найдите нок,нод 18,45;30,40...