Алгебра, вопрос задал Аноним , 6 лет назад

найдите производную функцию​

Приложения:

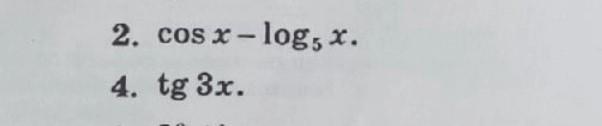
Ответы на вопрос

Ответил ЯковПервый
1

Номер 2:

f(x) = cos(x) - log_5x\\f'(x) = -sin(x) - \frac{1}{ln(5)*x}

Номер 4:

f(x) = tg(3x)\\f'(x) = \frac{1}{cos^2(3x)} * (3x)' = \frac{1}{cos^2(3x)} * 3 = \frac{3}{cos^2(3x)}

Замечание: все производные табличные, важно только не забыть про правило производной суммы ((f(x) + g(x))' = f'(x) + g'(x)) и правило производной сложной функции (f(g(x))' = f'(x)*g'(x))

Предыдущий вопрос
Следующий вопрос
Новые вопросы
Русский язык, 1 год назад
Помогите пожалуйста,нигде не могу найти ответ...
Русский язык, 1 год назад
изложение по рассказу Пушкина "метель"...
Математика, 6 лет назад
9 После завтрака Катя поиграла с сестрой в настольную игру, погуляла с подругой и испекла пирог в духовке. На каждое из этих занятий она потратила по часу, а потом пошла обедать вместе со всей...
Математика, 6 лет назад
Найди значения буквеных выражений b+2 b-2...
Литература, 8 лет назад
Написать рассказ (на одну страницу) если бы Электроник пришёл к тебе в класс. тоесть рассказать как бы ты с ним поступил.(дружил) срочно!!!
Физика, 8 лет назад
Помогите пожалуйста Хоть на что-то...