Найдите площадь треугольника, ограниченного прямыми y+x=0, y−x−4=0 и 2x+y−4=0.

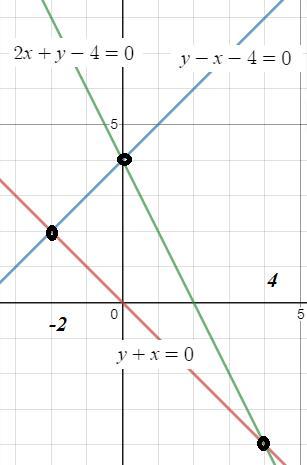
Найдем точки пересечения прямых:

(-2;2)  или (4;-4) или (0;4)

На [-2:0]  фигура ограничена    прямыми y=x+4 сверху  и снизу y=-x

На [0:4]  фигура ограничена    прямыми y=-2x+4 сверху  и снизу y=-x

S=∫⁰₋₂(x+4-(-x))dx+∫⁴₀(-2x+4-(-x))dx=

=∫⁰₋₂(2x+4)dx+∫⁴₀(-x+4)dx=

=(x²+4x)|⁰₋₂ + ((-x²/2)+4x)|⁴₀=

=0-(4-8)+(-8+16)=4+8=12

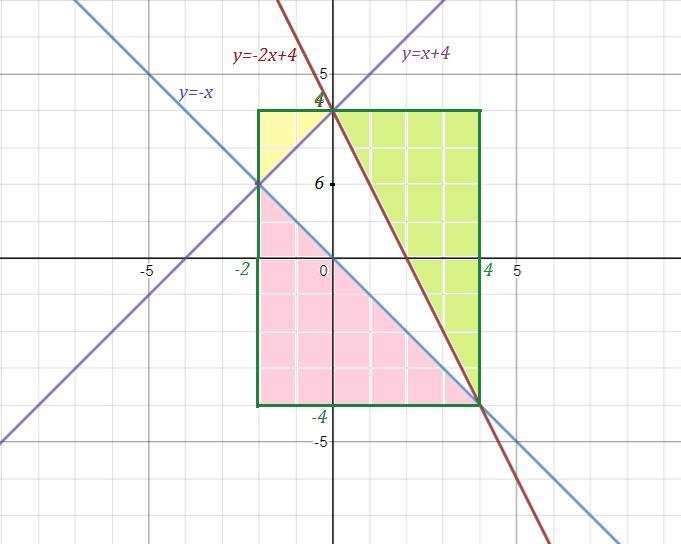
Три прямые при пересечении образуют треугольник. Достроим его до прямоугольника размером 6 на 8 . Тогда площадь заданного треугольника равна разности площадей прямоугольника и трёх прямоугольных треугольников (розового, жёлтого и зелёного).