Математика, вопрос задал Умка1011 , 8 лет назад

Найдите площадь трапеции у которой параллельные стороны 60 см и 20 см а непараллельные 13 см и 37 см

Ответы на вопрос

Ответил Аноним

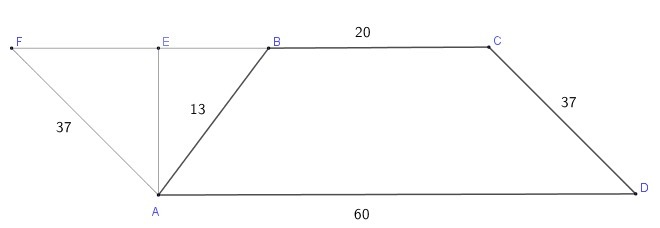
Продлим стороны до параллелограмма AFCD; FA = CD = 37 см и FC = AD = 60 см. Отрезок FB = FC - BC = 60 - 20 = 40 см. Найдем площадь треугольника AFB по формуле Герона:

$rm p=dfrac{FA+FB+BA}{2}=dfrac{37+40+13}{2}=45$ см - полупериметр

$rm S_{AFB}=sqrt{p(p-a)(p-b)(p-c)}=sqrt{45cdot(45-40)cdot(45-37)cdot(45-13)}=\ \ =sqrt{45cdot5cdot8cdot32}=sqrt{3^2cdot5^2cdot8^2cdot2^2}=3cdot5cdot8cdot2=240~_{CM^2}$

С другой стороны площадь треугольника равна $rm S_{AFB}=dfrac{FBcdot AE}{2}$ откуда высота $rm AE=dfrac{2S}{FB}=dfrac{2cdot240}{40}=12$ см. Высота треугольника AFB равна высоте трапеции, тогда