Найдите площадь равнобедренной трапеции с углом 45 градусов , меньшим основанием равным 7 и высотой 5. СРОЧНО ПОМОГИТЕ Я ДАМ ЕЩЕ БАЛЛОВ ТОЛЬКО ПОМОГИТЕЕЕЕЕЕЕЕЕЕЕЕ

Ответ:

Площадь равнобедренной трапеции равна 60 см²

Объяснение:

УСЛОВИЕ: Найдите площадь равнобедренной трапеции с углом 45 градусов , меньшим основанием равным 7 и высотой 5.

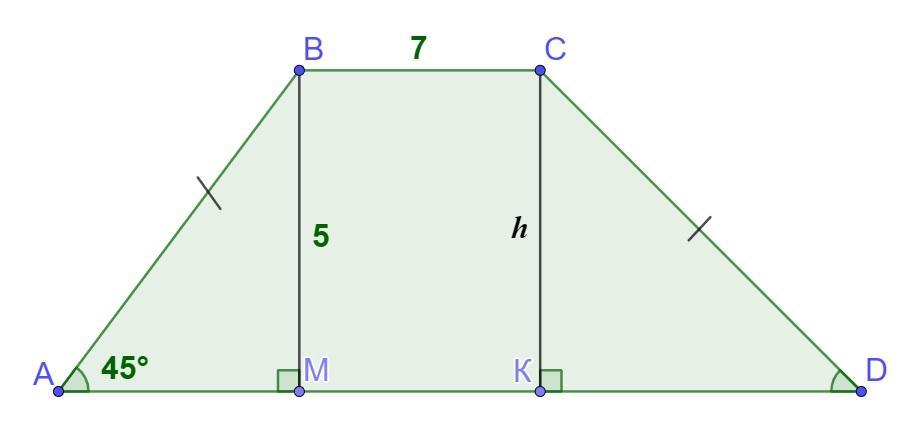
ДАНО: ABCD - трапеция, AD||BC, AB=CD, BМ⊥AD, СК⊥AD где BМ=СК=5 см – высота трапеции, опущенная на сторону AD, ВС=7 см, ∠А=45°

НАЙТИ: S(ABCD)

РЕШЕНИЕ:

1.

Рассмотрим прямоугольный треугольник  ABМ (∠AМB=90°).

По свойству острых углов прямоугольного треугольника:

∠А + ∠АВМ = 90°

∠АВМ = 90° - ∠А = 90° - 45° = 45°

∠А = ∠АВМ = 45° ⇒ ΔАВМ - равнобедренный с основанием АВ.

АМ = ВМ = 5 см - как боковые стороны равнобедренного треугольника.

2.

Рассмотрим прямоугольные треугольники ABМ и DСК.

У них:

• ∠А = ∠D - как углы при основании равнобедренной трапеции
• АВ = СD - как боковые стороны равнобедренной трапеции

Поэтому, по признаку равенства прямоугольных треугольников, ΔABМ =  ΔDСК (по гипотенузе и острому углу) , отсюда следует

AМ = KD = 5 см.

3.

Так как МВСК - прямоугольник, то МК = ВС = 7 см - как противоположные стороны прямоугольника.

Отсюда АD = АМ + МК + КD = 5 + 7 + 5 = 17 (см)

4.

Найдём площадь трапеции ABCD.

(см²)

ОТВЕТ: 60 см²

#SPJ1