Найдите площадь равнобедренного треугольника, если его боковая сторона равна 2a, а угол при основании 2b
Ответы на вопрос
Ответил orjabinina
1
Найдите площадь равнобедренного треугольника, если его боковая сторона равна 2a, а угол при основании 2b
Объяснение:
1 cgjcj,
Площадь треугольника равна половине произведения двух сторон умноженная на синус угла между ними.
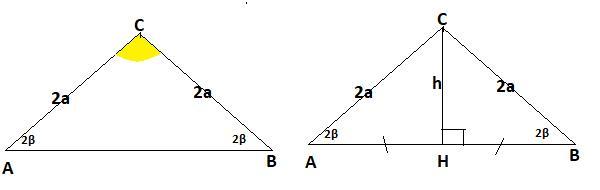
Тк. ΔАВС-равнобедренный ,то СА=СВ=2а и ∠А=∠В=2β ⇒∠АСВ=180°-4β
S=1/2*СА* СВ*sin∠АСВ , S=1/2*2а*2а*sin( π-4β)=2а²sin( π-4β) , S=2а²sin4β.
2 способ.
Пусть СН ⊥АВ , тогда АН=НВ по свойству равнобедренного треугольника . S=1/2*a*h, где а=АВ , h=СН
ΔАСН-прямоугольный , АС=2а, ∠А=2β
- sin ∠A=CH/AC ⇒ h=2a*sin2β ;
- cos∠A=AH/AC⇒ AH=2a*cos2β , значит АВ=4а*cos2β.
S=1/2*4acos2β*2asin2β= 2a²*2 cos2β*sin2β =2a²sin4β.
=================================
Формула приведения sin( π-α)=sinα
Приложения:
Новые вопросы
Русский язык,
1 год назад
Українська література,
2 года назад
Алгебра,
7 лет назад
Алгебра,
7 лет назад