найдите площадь прямоугольной трапеции,острый угол которой =30 градусов,а большая боковая сторона-8 см,если в эту трапецию можно вписать круг.
Ответы на вопрос
Ответил Аноним
2
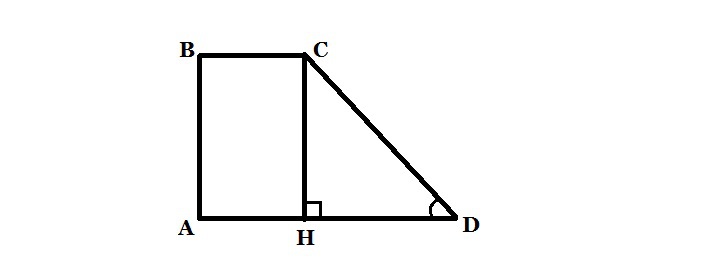
Проведем высоту СH (см. приложение). Так как в прямоугольном треугольнике CHD угол CDH = 30°, то катет СH, лежащий против этого угла, равен половине гипотенузы CD: CH = CD÷2 = 8÷2 = 4 см. Так как СH = AB, как высоты трапеции, то сумма противоположных сторон AB + CD = 12 см. Так как в трапецию можно вписать окружность, то суммы противоположных сторон должны быть равны, значит, AD + BC = 12 см. Найдем площадь по формуле: (AD + BC)÷2*AB = 6*4 = 24 см².
Приложения:
Новые вопросы
Українська мова,
1 год назад
Английский язык,
1 год назад
Геометрия,
1 год назад
Математика,
7 лет назад
Биология,
7 лет назад