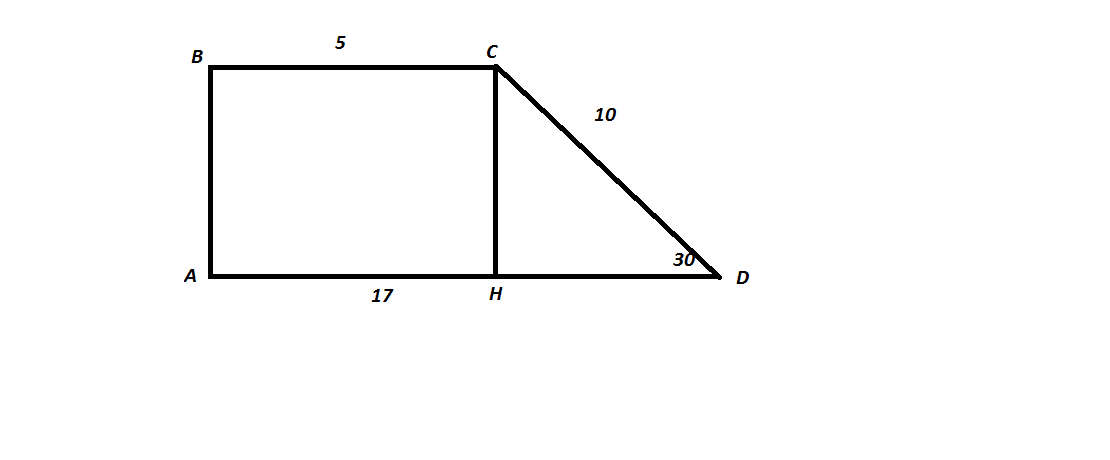
Найдите площадь прямоугольной трапеции,основания которой равны 5 см и 17 см,большая боковая сторона 10см,а меньший угол равен 30 градусов
Ответы на вопрос
Ответил DrunkHedgehog
0
Проведем высоту CH.
В треугольнике CDH найдем CH.
sinCDH=CH/CD
sin30=CH/CD
CH=CD*sin30=10*(1/2)=5 см
Тогда площадь см²
см²
В треугольнике CDH найдем CH.
sinCDH=CH/CD
sin30=CH/CD
CH=CD*sin30=10*(1/2)=5 см
Тогда площадь
Приложения:
Ответил leigrup
0
Обозначим трапецию АВСД. ВС=5, АД=17, СД=10. угол а - прямой. уголД=30 град. Из точки С опустим высоту СМ к АД. Треугольник СДМ прямоугольный. В прямоугольном треугольнике катет, лежащий против угла в 30 град в 2 раза меньше гипотенузы. Значит СМ=10/2=5 см. Площадь трапеции равна полусумме основаниий* на высоту.S=1/2*(ВС+АД)*СМ=1/2(5+17)*5=55
Приложения:

Новые вопросы