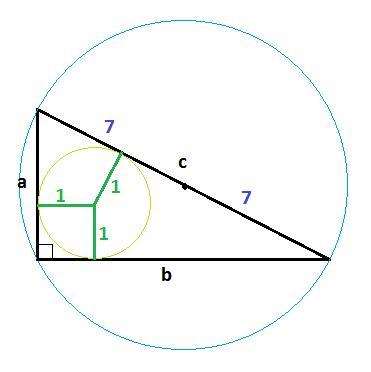
Найдите площадь прямоугольного треугольника,если радиусы вписанной в него и описанной около него окружностей r и R равны: r=1 см,R=7 см.

Дано : прямоугольный треугольник;

           с - гипотенуза,  r = 1 см,  R = 7 см

Найти : S

Решение :

Центр окружности, описанной около прямоугольного треугольника, находится на середине гипотенузы. Радиус равен половине гипотенузы.

см

Радиус окружности, вписанной в прямоугольный треугольник, можно посчитать по формуле

,   где p - полупериметр треугольника.

см

Площадь треугольника

см²

Ответ : 15 см²