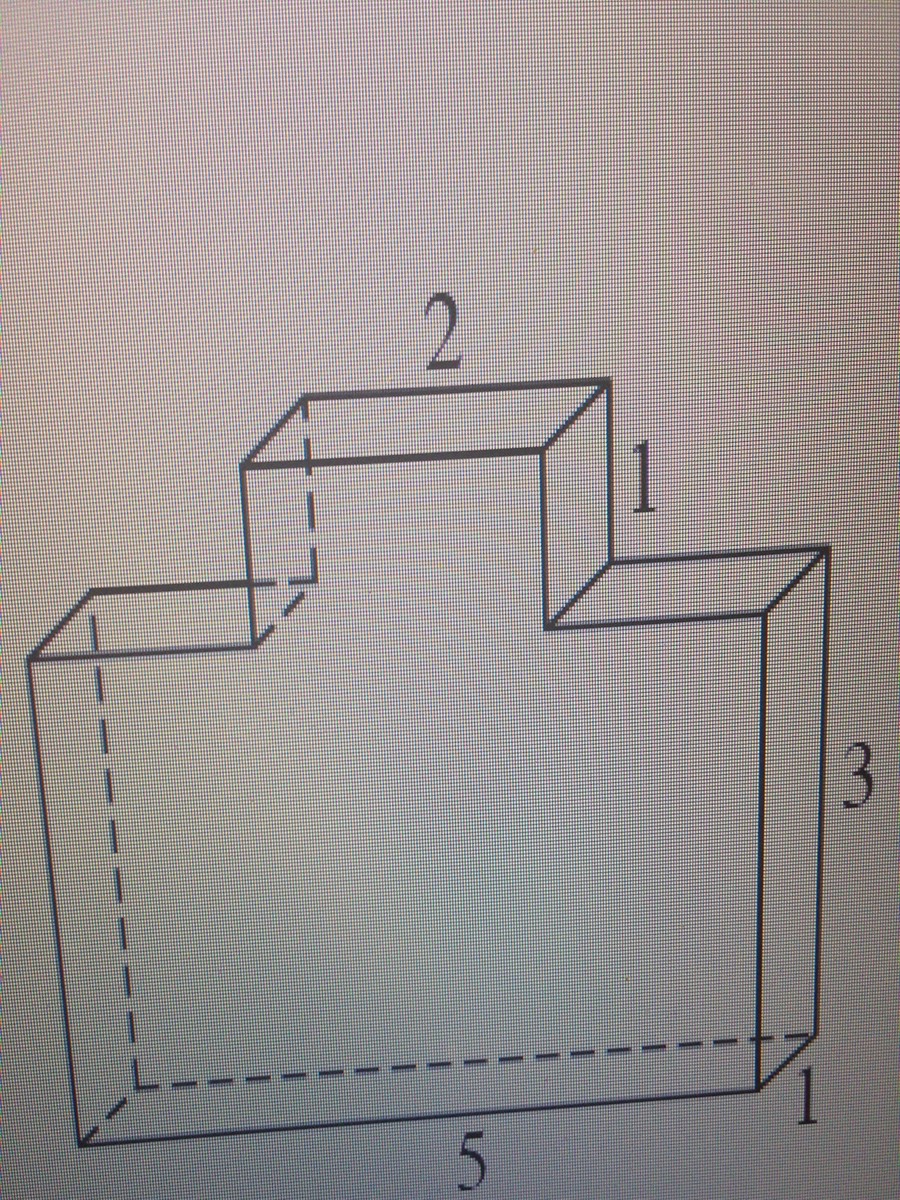
Найдите площадь поверхности многогранника, изображенного на рисунке (все доигранные углы прямые)

Данный многогранник можно разделить на два параллелепипеда.
Площадь  боковой поверхности  большего параллелепипеда равна произведению его высоты на периметр основания.
Высота=3
Периметр основания 2(ш+д)=2*(5+1)=12
S бок= 3*12=36
Площадь 2-х оснований равна 2*(5+1)=10.
Но из этой площади следует вычесть часть, которая закрыта меньшим параллелепипедом. Это площадь прямоугольника 2*1.
Т.е. S осн=10-2=8
Следовательно, площадь открытой поверхности большего параллелепипеда равна 36+8=44
Площадь боковой поверхности меньшего параллелепипеда 
S бок=2*(2+1)*1=6
S основания ( одного, второй закрыто) равна 2*1=2
Площадь открытой поверхности меньшего параллелепипеда 6+2=8
Общая площадь 44+8=52
----
Можно не вычитать из площади большего закрытый кусочек верхнего основания, а прибавить к его площади площадь только  боковой поверхности меньшего параллелепипеда. Результат будет тем же.