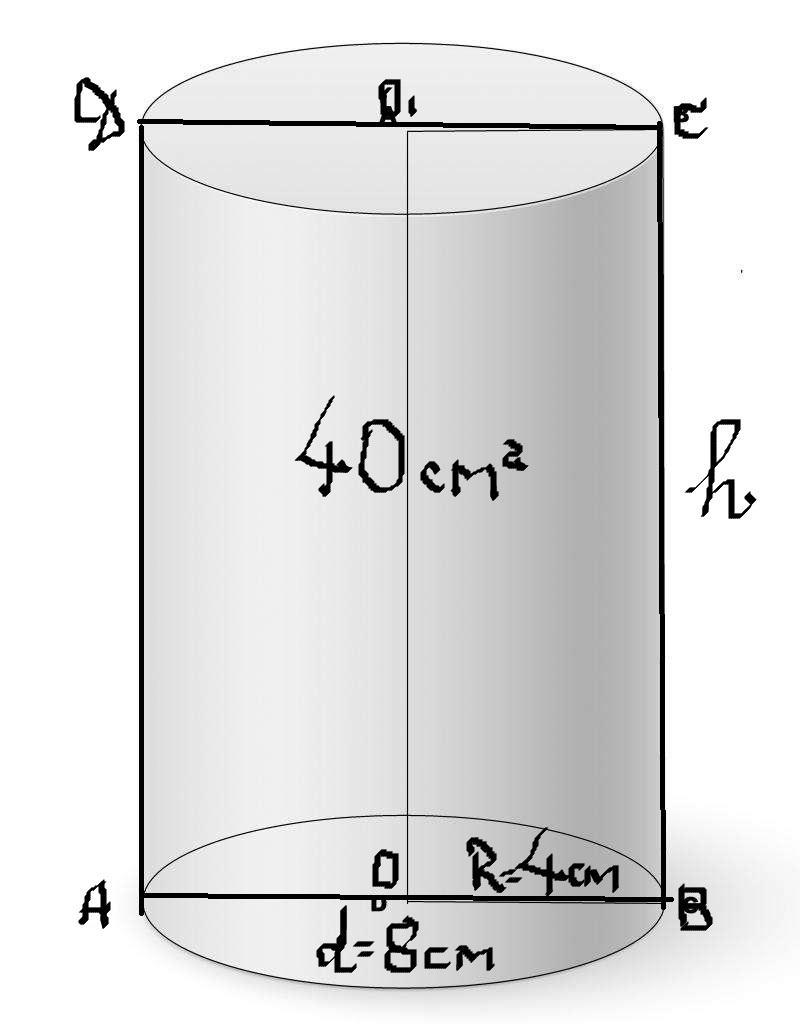
Найдите площадь полной поверхности цилиндра с радиусом 4см и площадью осевого сечения 40 см^2
Ответы на вопрос
Ответил sergeevaolga5
1
Ответ:
72π см²
Пошаговое объяснение:
Sпов.=2Sосн.+Sбок.
Sосн.=πR²
Sбок.=2πRh
Sпов. = 2πR+2πRh=2πR(R+h), где R- радиус, h - высота цилиндра
R=4 см, Sос.сеч. = 40 см²
S ос.сеч=S(АВСД)
АВСD - прямоугольник, поэтому S(ABCD) = AB*BC=2BO*BC=2R*h
2Rh=40
2*4h=40
8h=40
h=5 (см) - высота цилиндра
Находим площадь полной поверхности цилиндра:
Sпов. = 2πR(R+h)=2π*4(4+5) =8π*9 =72π (см²)
Приложения:
Новые вопросы
Французский язык,
1 год назад
Физика,
1 год назад
Литература,
1 год назад
Математика,
1 год назад
Литература,
6 лет назад