найдите площадь плоской фигуры. ограниченными линиями y=3-x^2 ,y=2
Ответы на вопрос
Ответил Nennn
0
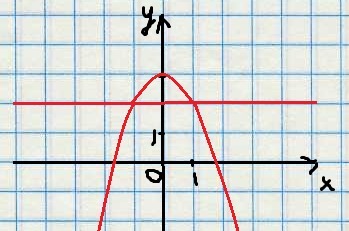
1. Построим на одном графике функции y=3-x^2 и y=2.
2. Найдем точки пересечения (пределы интегрирования). Для этого решим систему уравнений.

3. Парабола лежит выше прямой, поэтому при интегрировании будем вычитать из функции y=3-x^2 функцию y=2.

Ответ: 4/3.
2. Найдем точки пересечения (пределы интегрирования). Для этого решим систему уравнений.
3. Парабола лежит выше прямой, поэтому при интегрировании будем вычитать из функции y=3-x^2 функцию y=2.
Ответ: 4/3.
Приложения:
Новые вопросы