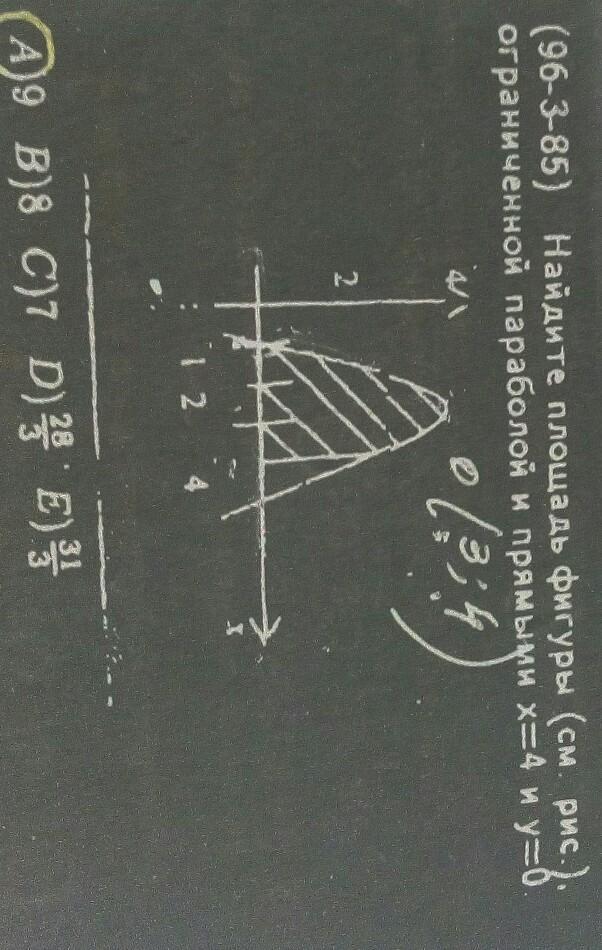
Алгебра, вопрос задал Роман1233212002 , 7 лет назад

Найдите площадь фигуры. (см рис). С объяснением!

Приложения:

Ответы на вопрос

Ответил NNNLLL54

Уравнение параболы, симметричной оси х=х₀ с вершиной в точке (х₀,у₀):

$y-y_0=pm 2p(x-x_0)^2$ .

Вершина заданной параболы в точке О(3;4), ось симметрии х=3:

$y-4=-(x-3)^2; ; Rightarrow ; ; ; y=-x^2+6x-5\\S=intlimits^4_1, (-x^2+6x-5), dx=(-frac{x^3}{3}+3x^2-5x)Big |_1^4=\\=-frac{64}{3}+48-20-(-frac{1}{3}+3-5)=-21+28+2=9$

P.S. Уравнение параболы можно вывести, зная вершину параболы (3,4) и две точки пересечения с осью ОХ - это точки (1,0) и (5,0). Подставить координаты в уравнение y=ax²+bx+c. Получится система трёх уравнений.

Ответил NNNLLL54

Чтобы это понять, нарисуй бОльшую кривол. трапецию, ограниченную линиями: { y=2x, x=2 , y=0 } - это треугольник , и мЕньшую кривол. трапецию: {y=x^2 , y=0 , x=2 } . А затем совмести рисунки и увидишь, что площадь заданной области (не кривол. трапеции) равна разности площадей кривол. трапеций.

Ответил Роман1233212002

аа вот в чём дело, понятно

Ответил Роман1233212002

Всегда отнимается от большей площади меньшую?

Ответил NNNLLL54

да, все забывают про то, что означает термин " криволинейная трапеция"...

Ответил NNNLLL54

конечно, отнимают от большей площади меньшую, ведь площадь области не может быть отрицательной.

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Английский язык, 1 год назад