Найдите периметр равнобедренного трапеции, основания которой равны 7 см и 25 см, а диагонали перпендикулярны к боковым сторонам
Ответы на вопрос
Ответил Пеппер
0
Ответ:
62 см.
Объяснение:
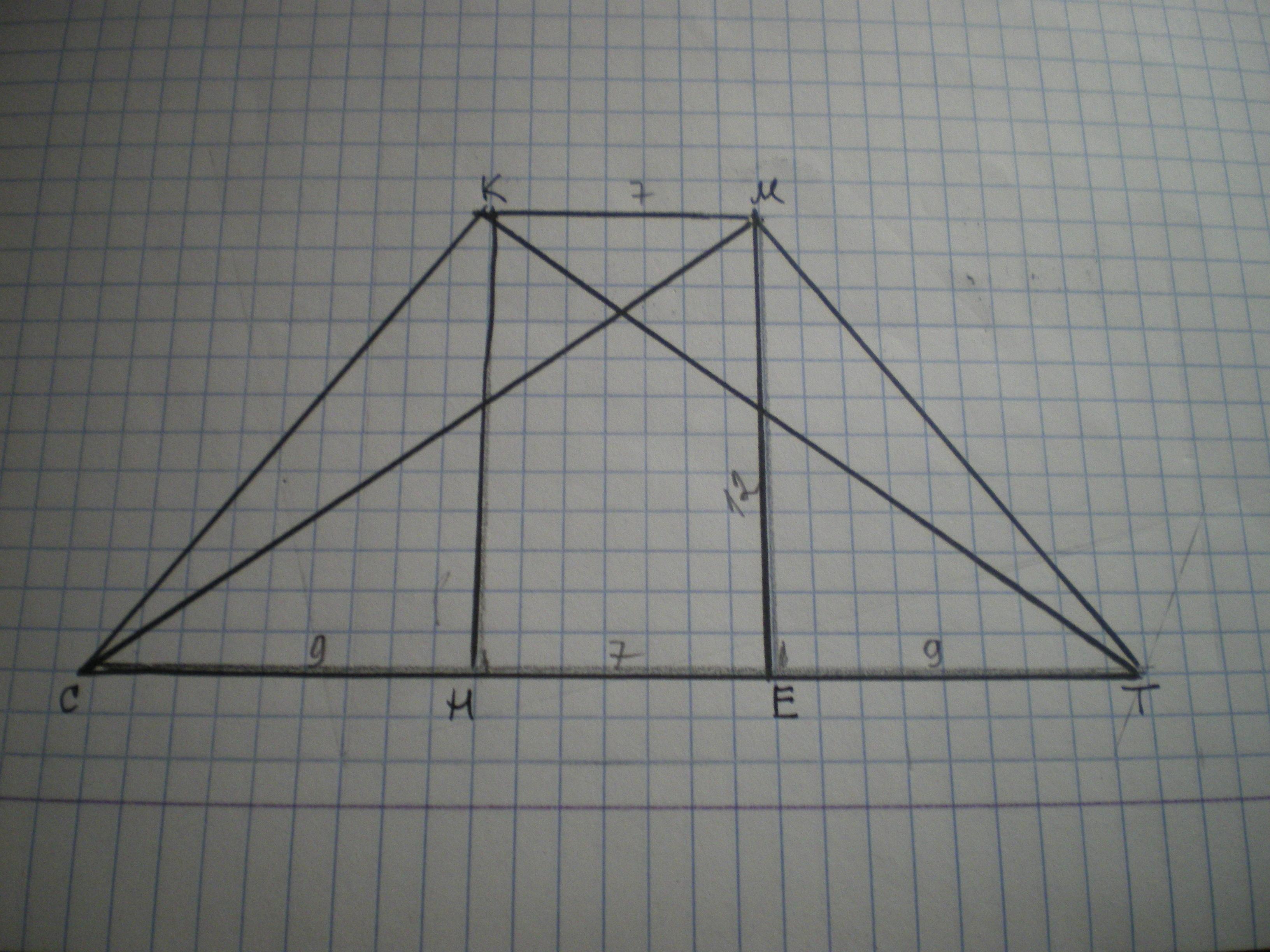
Дано: СКМТ - трапеция, СК=МТ, СМ⊥МТ, КТ⊥КС, КМ=7 см, СТ=25 см. Найти Р(СКМТ).
Проведем высоты КН и МЕ.
КМЕН - прямоугольник, поэтому ЕН=МК=7 см.
ΔСКН=ΔТМЕ по гипотенузе и острому углу, поэтому и СН=ТЕ=(25-7):2=9 см.
СЕ=СН+ЕН=9+7=16 см.
По свойству высоты, проведенной из вершины прямого угла к гипотенузе, МЕ=√(СЕ*ЕТ)=√(16*9)=4*3=12 см.
Рассмотрим ΔЕМТ, по теореме Пифагора
МТ=√(МЕ²+ЕТ²)=√(144+81)=√225=15 см.
Р=КМ+МТ+СТ+СК=7+15+25+15=62 см.
Приложения:
Новые вопросы