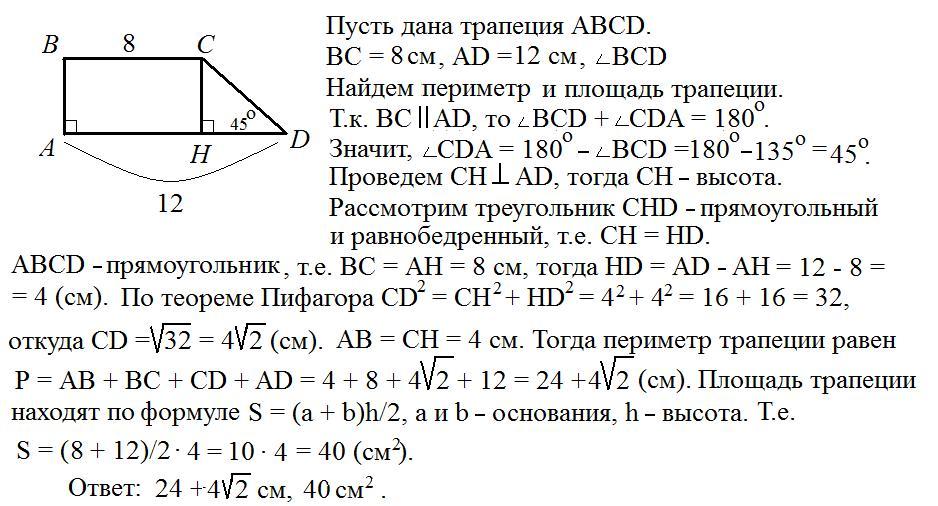
найдите периметр и площадь прямоугольной трапеции, если длины ее оснований равны 8 см и 12 см, а один из углов равен 135°

заранее спасибо :)
​

Дано :

Четырёхугольник ABCD - прямоугольная трапеция (∡А = ∡В = 90°).

ВС = 8 см.

AD = 12 см.

∡BCD = 135°.

Найти :

S(ABCD) = ?

P(ABCD) = ?

Решение :

Проведём из вершины С к основанию AD высоту СЕ.

Рассмотрим ΔCED - прямоугольный. По свойству трапеции ∡BCD + ∡CDA = 180° (это не сложно доказать, так как основания параллельны, а ∡BCD и ∡CDA - односторонние). Поэтому, ∡CDA = 180° - ∡BCD = 180° - 135° = 45°. А если у прямоугольного треугольника один из острых углов равен 45°, то такой прямоугольный треугольник - равнобедренный. Следовательно, ΔCED - не только прямоугольный, но и равнобедренный (ED = EC).

Рассмотрим четырёхугольник ABCE.

• Если у четырёхугольника три угла прямые, то этот четырёхугольник - прямоугольник.

Так как ∡А = ∡В = ∡СЕА = 90°, то четырёхугольник АВСЕ - прямоугольник.

• Противоположные стороны прямоугольника равны.

Следовательно, ВС = АЕ = 8 см.

AD = AE + ED

12 см = 8 см + ED

ED = 12 см - 8 см = 4 см.

ED = EC = 4 см.

Гипотенузу прямоугольного треугольника можно вычислить по формуле -

Где а - это катет равнобедренного прямоугольного треугольника.

Тогда -

CD = 4√2 см.

• Площадь трапеции равна произведению полусуммы оснований и высоты.

Следовательно -

S(ABCD) = 40 (см²).

- - -

Теперь найдём периметр. Периметр - это сумма длин всех сторон.

• В прямоугольной трапеции высота равна меньшей боковой стороне.

В нашем случае меньшая боковая сторона - это сторона АВ.

То есть -

АВ = ЕС = 4 см.

Тогда -

P(ABCD) = 4*(6 + √2) см.

Ответ :

40 см², 4*(6 + √2) см.

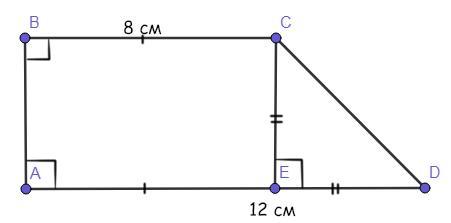
См. решение на рисунке.