Найдите пары равных треугольников и докажите их равенство.

Ответы на вопрос
7 задание
Рассм. пятиугольник RMTNS
угол M= углу N
угол TRS = углу TSR ⇒ TR=TS
Расс. тр-к RMS и RNS
- угол M= углу N
- угол TRS = углу TSR
- RS общая
Отсюда треугольники равны по стороне и двум углам
Рассм. тр-к RMT и TNS
- TR=RS (угол TRS = углу TSR)
- угол M= углу N
- угол MTR = углу NTS (вертикальные)
Отсюда треугольники равны по двум углам и стороне
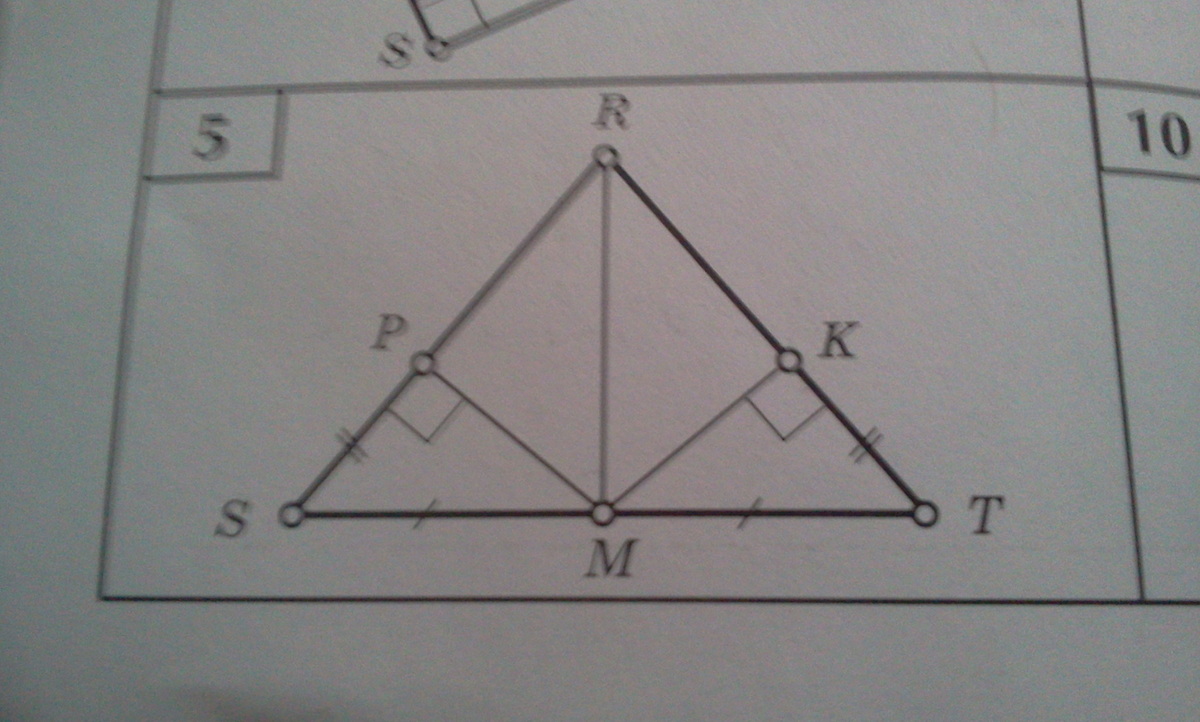
5 задание
Рассм. тр SPM и MKT
- PS=KT
- SM=MT
- угол P = углу К
Отсюда треугольники равны по двум сторонам и углу
Рассм.SRM и MRT
- угол S = углу T (тр-к SPM = MKT)
- RM - общая
- SM=MT
Отсюда треугольники равны по двум сторонам и углу
Рассм. PRM и RKM
- угол PRM = углу MRK (тр-к SPM = MKT⇒ SRT равнобед. RM высота и бисс)
- угол P = углу K = 90
- RM общая
отсюда треугольники равны по стороне и двум углам
7
равные RMS = SRN
<M=<N=90 град -по условию
RMS ; SRN -прямоугольные
<NRS=<MSR -по условию - острые углы
RS - общая сторона - гипотенуза
по 3-му признаку равенства прямоугольного треугольника
Если гипотенуза и острый угол одного прямоугольного треугольника соответственно равны гипотенузе и острому углу другого прямоугольного треугольника, то такие треугольники равны.
RMS = SRN - равные
из первого равенства следует
стороны MR=NS - катеты
<M=<N=90 град -по условию
RMT ; SNT -прямоугольные
<MTR = <NTS - вертикальные
<MRT = 90-<MTR
<NST = 90 - <NTS
значит <MRT = <NST
по 2-му признаку равенства прямоугольного треугольника
Если катет и прилежащий к нему острый угол одного прямоугольного треугольника соответственно равны катету и прилежащему острому углу другого прямоугольного треугольника, то такие треугольники равны.
RMT = SNT -равные
5
равные PMS = KMT
<SPM=<TKM=90 град -по условию
PMS ; KMT -прямоугольные
SM=MT - по условию - гипотенузы
SP=KT -по условию - катеты
по 4-му признаку равенства прямоугольного треугольника
Если гипотенуза и катет одного прямоугольного треугольника соответственно равны гипотенузе и катету другого прямоугольного треугольника, то такие треугольники равны.
PMS = KMT - равные
из первого (равные PMS = KMT) следует
< MSP =<MTK
SM=MT - по условию
STR - равнобедренный
далее можно доказать
RPM =RKM - равны
RMS = RMT -равны