Найдите область определения функции
СРОЧНО
ПОЖАЛУЙСТА
Приложения:
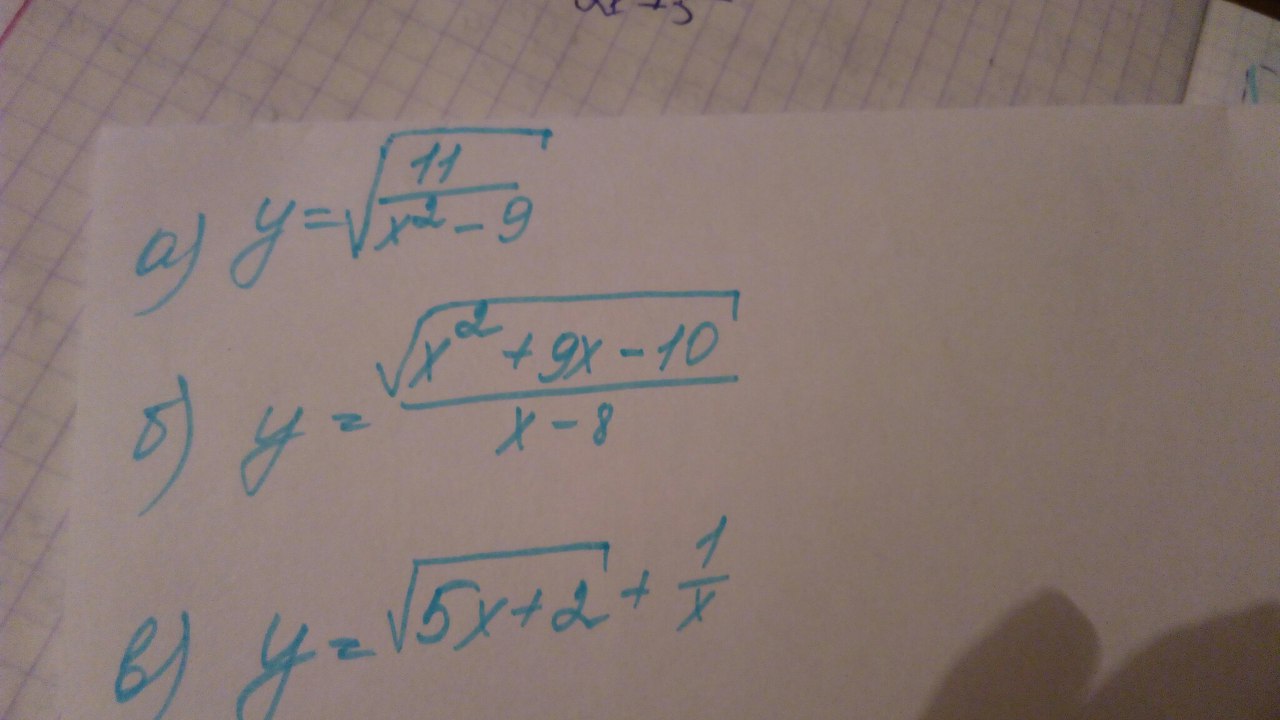

Ответы на вопрос
Ответил m11m
0
a)

ОДЗ:
x²-9>0
(x-3)(x+3)>0
x=3 x=-3
+ - +
------- -3 ----------- 3 -----------
\\\\ \\\\\\
x∈(-∞; -3)U(3; +∞)
D(y)=(-∞; -3)U(3; +∞)
б)

ОДЗ:
1) x²+9x-10≥0
x²+9x-10=0
D=9² -4*(-10)=81+40=121=11²
x₁=(-9-11)/2=-10
x₂=(-9+11)/2=1
(x+10)(x-1)≥0
+ - +
---------- -10 ---------- 1 -----------
\\\\\\ \\\\\\\
x∈(-∞; -10]U[1; +∞)
2) x-8≠0
x≠8
В итоге ОДЗ: x∈(-∞; -10]U[1; 8)U(8; +∞)
D(y)=(-∞; -10]U[1; 8)U(8; +∞)
в)

ОДЗ:
1) 5x+2≥0
5x≥ -2
x≥ -0.4
2) x≠0
В итоге ОДЗ: x∈[-0.4; 0)U(0; +∞)
D(y)=[-0.4; 0)U(0; +∞)
a)

ОДЗ:
x²-10x+21≥0
x²-10x+21=0
D=(-10)²-4*21=100-84=16=4²
x₁=(10-4)/2=3
x₂=(10+4)/2=7
+ - +
-------- 3 ---------- 7 ------------
\\\\\ \\\\\\
x∈(-∞; 3)U(7; +∞)
D(y)=(-∞; 3)U(7; +∞)
б)

ОДЗ:
1) (x-3)(x+7)≥0
x=3 x= -7
+ - +
-------- -7 --------- 3 ----------
\\\\\ \\\\\\\
x∈(-∞; -7]U[3; +∞)
2) x-6≠0
x≠6
В итоге х∈(-∞; -7]U[3; 6)U(6; +∞)
D(y)=(-∞; -7]U[3; 6)U(6; +∞)
в)

ОДЗ:
1) x+5≥0
x≥ -5
2) 4x-2≠0
4x≠2
x≠0.5
В итоге ОДЗ: х∈[-5; 0.5)U(0.5; +∞)
D(y)=[-5; 0.5)U(0.5; +∞)
ОДЗ:
x²-9>0
(x-3)(x+3)>0
x=3 x=-3
+ - +
------- -3 ----------- 3 -----------
\\\\ \\\\\\
x∈(-∞; -3)U(3; +∞)
D(y)=(-∞; -3)U(3; +∞)
б)
ОДЗ:
1) x²+9x-10≥0
x²+9x-10=0
D=9² -4*(-10)=81+40=121=11²
x₁=(-9-11)/2=-10
x₂=(-9+11)/2=1
(x+10)(x-1)≥0
+ - +
---------- -10 ---------- 1 -----------
\\\\\\ \\\\\\\
x∈(-∞; -10]U[1; +∞)
2) x-8≠0
x≠8
В итоге ОДЗ: x∈(-∞; -10]U[1; 8)U(8; +∞)
D(y)=(-∞; -10]U[1; 8)U(8; +∞)
в)
ОДЗ:
1) 5x+2≥0
5x≥ -2
x≥ -0.4
2) x≠0
В итоге ОДЗ: x∈[-0.4; 0)U(0; +∞)
D(y)=[-0.4; 0)U(0; +∞)
a)
ОДЗ:
x²-10x+21≥0
x²-10x+21=0
D=(-10)²-4*21=100-84=16=4²
x₁=(10-4)/2=3
x₂=(10+4)/2=7
+ - +
-------- 3 ---------- 7 ------------
\\\\\ \\\\\\
x∈(-∞; 3)U(7; +∞)
D(y)=(-∞; 3)U(7; +∞)
б)
ОДЗ:
1) (x-3)(x+7)≥0
x=3 x= -7
+ - +
-------- -7 --------- 3 ----------
\\\\\ \\\\\\\
x∈(-∞; -7]U[3; +∞)
2) x-6≠0
x≠6
В итоге х∈(-∞; -7]U[3; 6)U(6; +∞)
D(y)=(-∞; -7]U[3; 6)U(6; +∞)
в)
ОДЗ:
1) x+5≥0
x≥ -5
2) 4x-2≠0
4x≠2
x≠0.5
В итоге ОДЗ: х∈[-5; 0.5)U(0.5; +∞)
D(y)=[-5; 0.5)U(0.5; +∞)
Новые вопросы