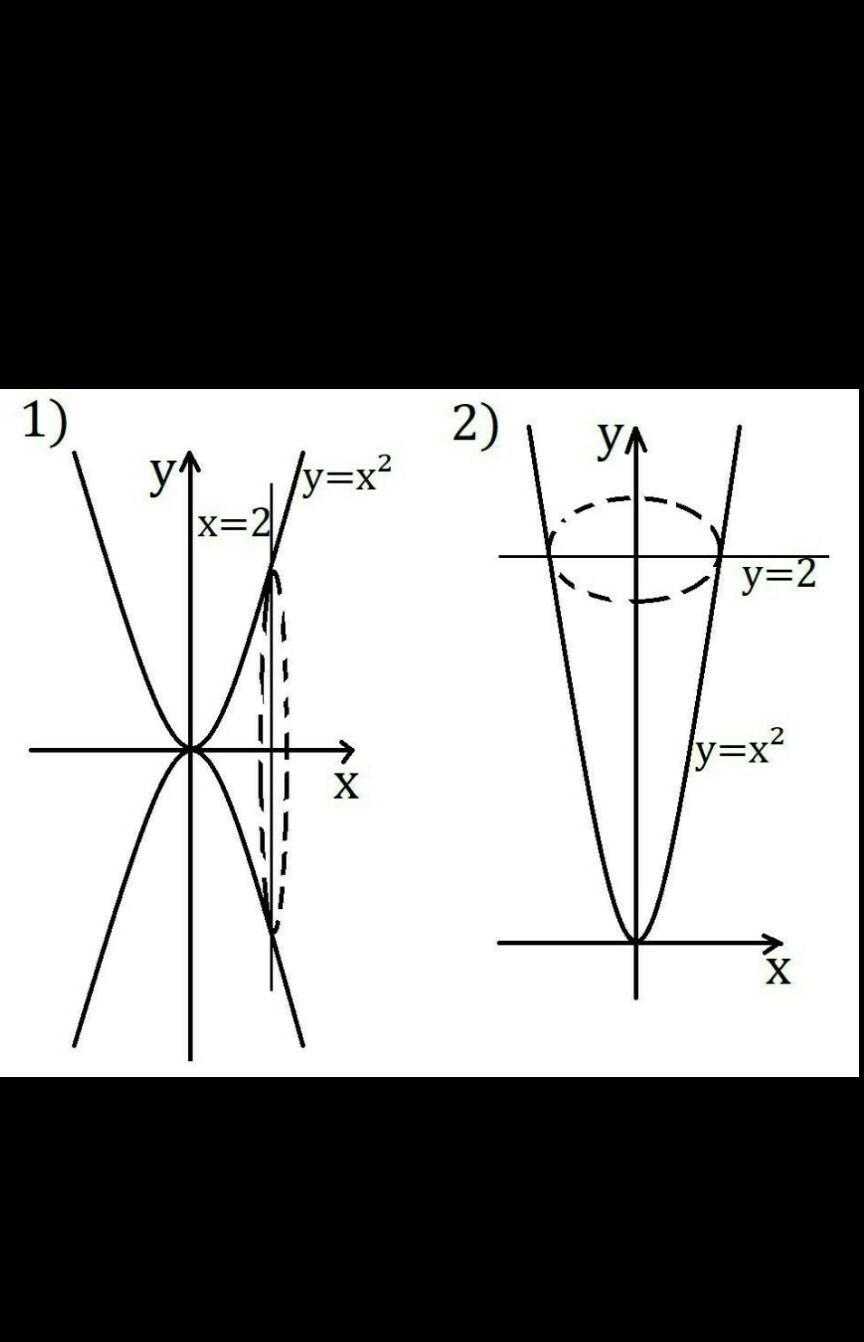
Найдите объем тела, полученного при вращении параболы у = х2 от точки х=0 до точки х=3 вокруг оси абсцисс.

Пошаговое объяснение:

Объём тела, полученного при вращении вокруг оси Ox фигуры, ограниченной линиями y=x², x=0, x=2, равен:

\begin{gathered}\tt \displaystyle V=\pi \int\limits^2 _0 y^2 \; dx=\pi \int\limits^2 _0 x^4 \; dx=\pi \cdot \begin{pmatrix}\frac{x^5}5\end{pmatrix} \begin{vmatrix}\\ \\ \end{matrix} ^2 _0 =\\ \\ \\ =\pi \begin{pmatrix}\frac{2^5}5 -\frac{0^5}5\end{pmatrix} =\frac{32}5 \pi =6,\! 4\, \pi\end{gathered}

Ответ: 6,4π.

2)

При x = -2, y = (-2)² = 4.

При x = 2, y = 2² = 4.

Надо найти объём тела, полученного при вращении вокруг оси Oy фигуры, ограниченной линиями y=x², y=4. \tt \displaystyle y=x^2 \rightarrow y_min =0y=x

2

→y

m

in=0

\begin{gathered}\tt \displaystyle V=\pi \int\limits^4 _0 x^2 \; dy=\pi \int\limits^4 _0 y \; dy=\pi \cdot \begin{pmatrix}\frac{y^2}2\end{pmatrix} \begin{vmatrix}\\ \\ \end{matrix} ^4 _0 =\\ \\ \\ =\pi \begin{pmatrix}\frac{4^2}2 -\frac{0^2}2\end{pmatrix} =8\pi \end{gathered}

Ответ: 8π.