Найдите наименьший острый угол прямоугольного треугольника , если известно , что медиана , выходящая из вершины прямого угла , делит этот угол в отношении 2:1
Ответы на вопрос
Ответил Rikza
0
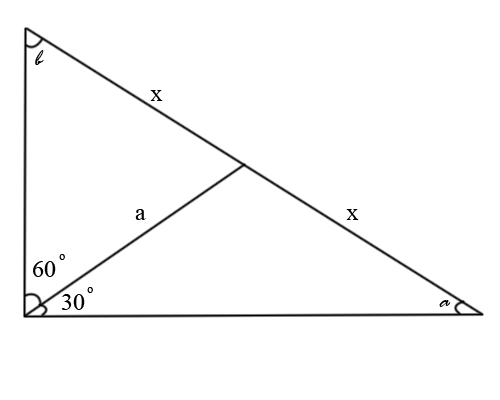
Пусть гипотенуза - 2х, медиана - а. Тогда получается (по свойствам синусов и сторон):
=
=
sin 30 = 1/2 sin 60 = /2
Выразив а из этих уравнений, можно их приравнять. Получаем:
2x*sin a =
Сократив 2х, выражаем синус одного угла через другой, т. е.
sin b = *sin a
Подбирая значения, получаем угол a = 30 градусам, b = 60
Ответ: наименьший угол равен 30 градусам. Смотри во вложении
Приложения:
Новые вопросы
Литература,
6 лет назад
История,
6 лет назад
Математика,
9 лет назад
Биология,
9 лет назад
Литература,
9 лет назад