Найдите наибольшее и наименьшее значение функции
a) y=-x^3+3x+3 на отрезках 1) [-1;2] 2) [1; 3] 3) [-1; 3]
b) y=x^33 - 5x^22 +6x+10 1) [0; 1] 2) [0; 2,5] 3) [0,4]
c) y=x^4-8x^2-9 1) [-1,1] 2) [0; 3] 3) [3;5]
Ответы на вопрос
а)
Дано: y = -x³ + 3*x+3
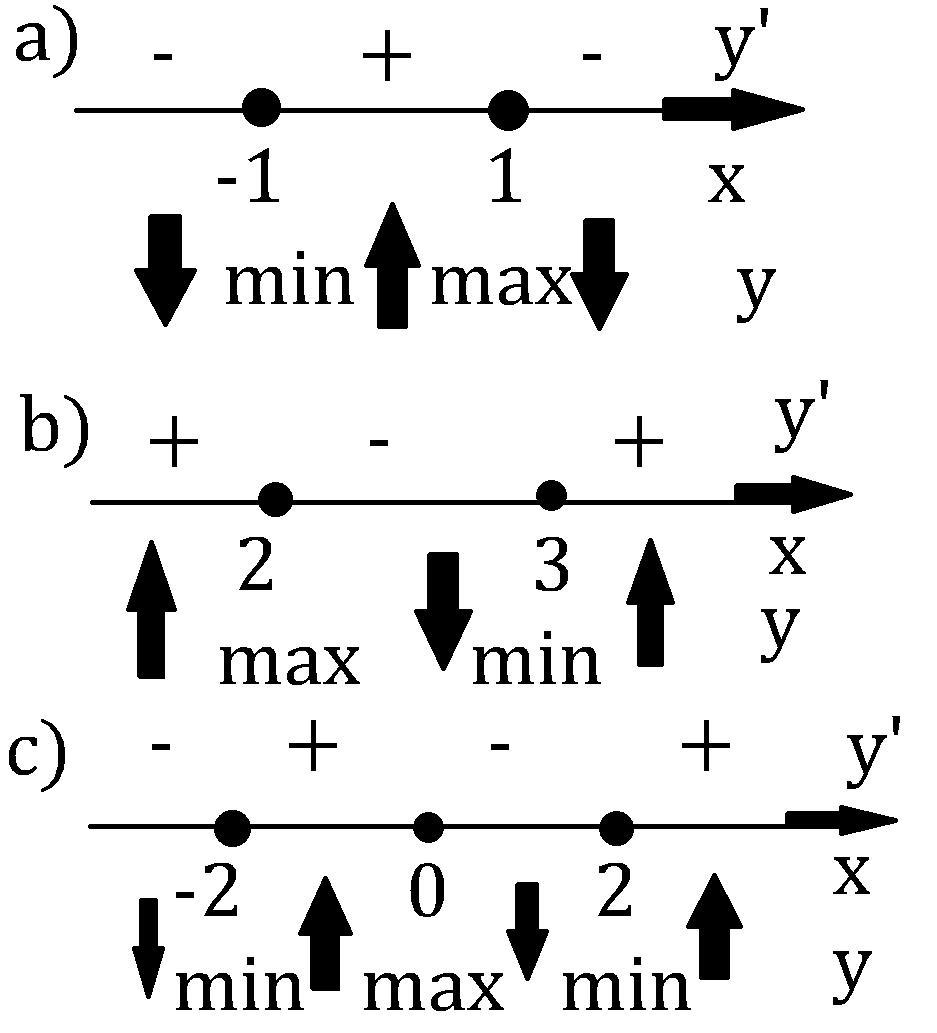
y'(x) = -3*x² + 3 = -3*(x²-1) = - 3*(x-1)*(x+1)= 0 - первая производная.
Корни: х1 = - 1 и х2 = 1 - точки экстремумов.
Вычисляем.
1) x = -1 ⇒ ymin = 1 , x = 1 ⇒ ymax = 5 - ответ
2) x = 1 ⇒ ymax = 5, x = 3 ⇒ ymin = -15 - ответ
3) x = -1 ⇒ ymax = 1 , x = 3 ⇒ ymin = -15 - ответ
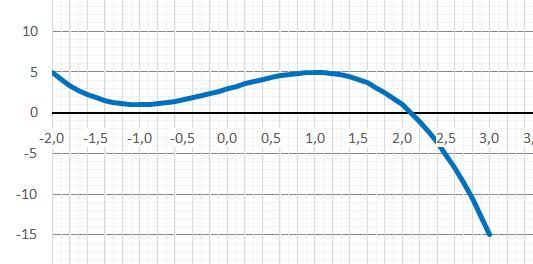
рисунок с графиком .
b) Дано: y = 1/3*x³ - 2.5*x² + 6*x +10
y'(x) = x² - 5x + 6 = (х-2)*(х-3) = 0 - находим корни.
х1 = 2, х2 = 3
1) ymin(0) = 10 ymax(1) = 13 5/6 - ответ
2) ymin(0) = 10 ymax(2,5) = 14 3/5 - ответ
3) ymin(0) = 10 ymax(4) = 15 1/3 - ответ
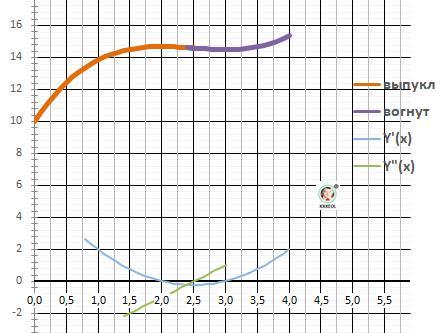
Рисунок с графиком.
с) Дано: y = x⁴ - 8*x² - 9
y'(x) = 4*x³ - 16*x = 4*x*(x-2)*(x+2) = 0
Экстремумы в точках? х1 = - 2, х2 = 0 , х3 = 2.
) ymin(-1) = -16 ymax(0) = -9 - ответ
2) ymin(0) = -9 ymax(3) = 0 - ответ
3) ymin(3) = 0 ymax(5) = 416 - ответ
Рисунок с графиком.

a)
1) [-1;2]
2) [1;3]
3) [-1;3]
b)
1) [0;1]
2) [0;2,5]
3) [0;4]
c) Степени чётные, поэтому функция чётная (с названиями просто совпадение), это значит, что y(x)=y(-x)
1) [-1;1]
2) [0;3]
3) [3;5]