Найдите наибольшее четырехзначное число которое при делении и на 80 и на 75 дает в остатке 23
Ответы на вопрос
Ответил platon1108
0
Здравствуйте!
Ответ:
9623
Пошаговое объяснение:
Если нужное нам число дает остаток 23 по делении 75 и 80, то число, которое получается при вычитании 23 из нужного нам, делится нацело и на 75, и на 80.
Найдем НОК чисел 75 и 80 (1 фото).
НОК (75; 80)= 1200.
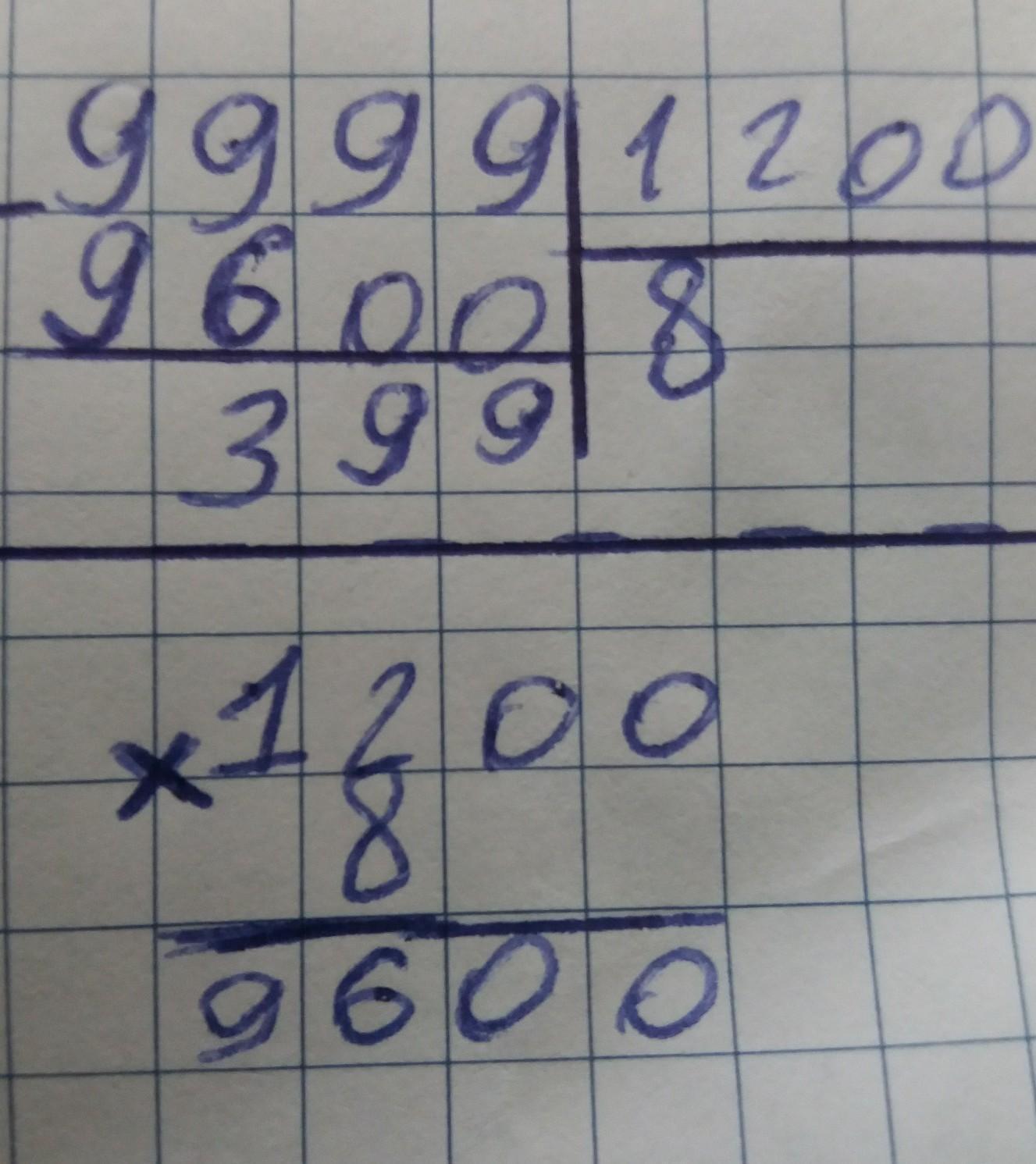
Теперь найдем наибольшее кратное числа 1200 среди 4-ёхзначных чисел. Для этого 9999 разделим на 1200 с остатком, а потом умножим целую часть кратного на 1200 (2 фото).
Получаем 9600. Это самое большое 4-ёхзначное число, которое делится и на 75, и на 80. А значит самое большое 4-ёхзначное число, которое делится и на 75, и на 80 с остатком 23 это:
9600+23=9623.
Приложения:
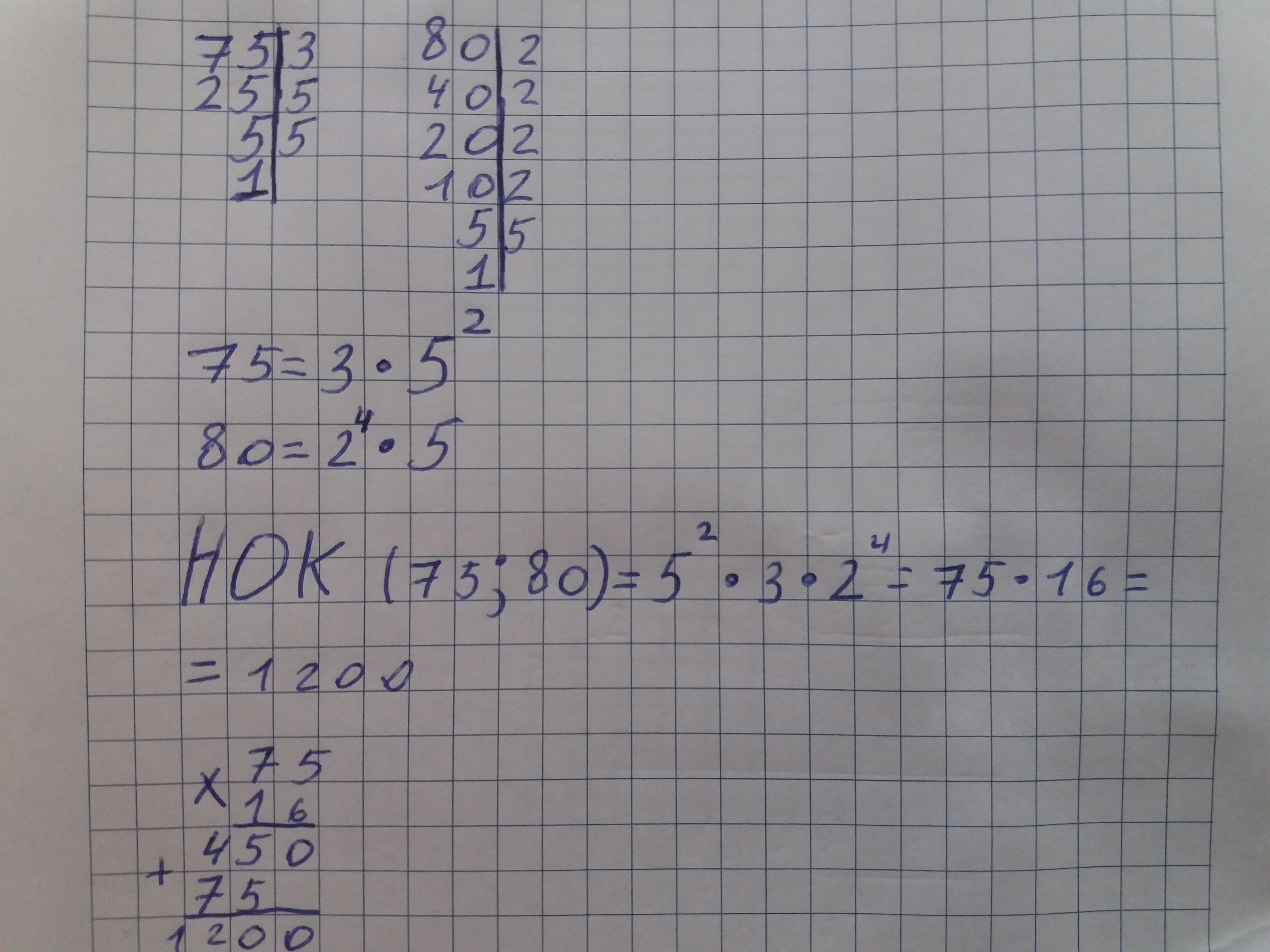
Новые вопросы