Алгебра, вопрос задал ananas7zzz7 , 6 лет назад

Найдите корень уравнения log7(4+13x)=log7(8-x)+1

Приложения:

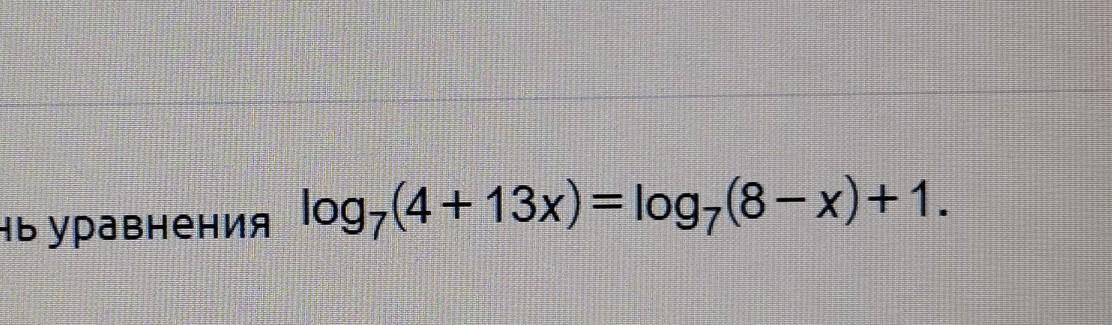
Ответы на вопрос

Ответил Vopoxov

Ответ:

х = 2,6

Объяснение:

$\log_{7}(4 + 13x) = \log_{7}(8 - x) + 1$

ОДЗ:

$\begin{cases}4 {+} 13x > 0 \: { < = >} \: x >{ - \dfrac{4}{13} }\\8 - x > 0 \: \: {< = > } \: \: x < 8 \end{cases} = > x{ \in}({ - } \frac{4}{13} ;\: 8)$

Т.к. по свойствам логарифмов

$\log_{a}a = 1$

$\log_{7}(4 + 13x) = \log_{7}(8 - x) + \log_{7}7 \\ \log_{7}(4 + 13x) = \log_{7}((8 - x){ \cdot}7)$

Т.к. равенство логарифмов подразумевает равенство подлогарифмических выражений (при условии учета ОДЗ), имеем

$4 + 13x= 7(8 - x) \\ 4 + 13x = 56 - 7x \\ 13x + 7x = 56 - 4 \\ 20x = 52 \\ x = \frac{52}{20} = 2.6$

Как видим, корень уравнения входит в ОДЗ:

$x = 2.6 \: \in \: ({ - } \tfrac{4}{13} ;\: 8) \\$

т. е. ответом будет

х = 2.6

Ответил mathkot

Ответ:

x = 2,6

Объяснение:

$\log_{7}{(4 + 13x)} = \log_{7}{(8 - x)} + 1$

ОДЗ: $\boxed{x \in \bigg (-\dfrac{4}{13};8 \bigg)}$

$\displaystyle \left \{ {{4 + 13x > 0} \atop {8 - x > 0}} \right \left \{ {{ 13x > -4|:13} \atop {8 > x}} \right \left \{ {{x > -\dfrac{4}{13} } \atop {8 > x}} \right. \Longrightarrow x \in \bigg (-\dfrac{4}{13};8 \bigg)$