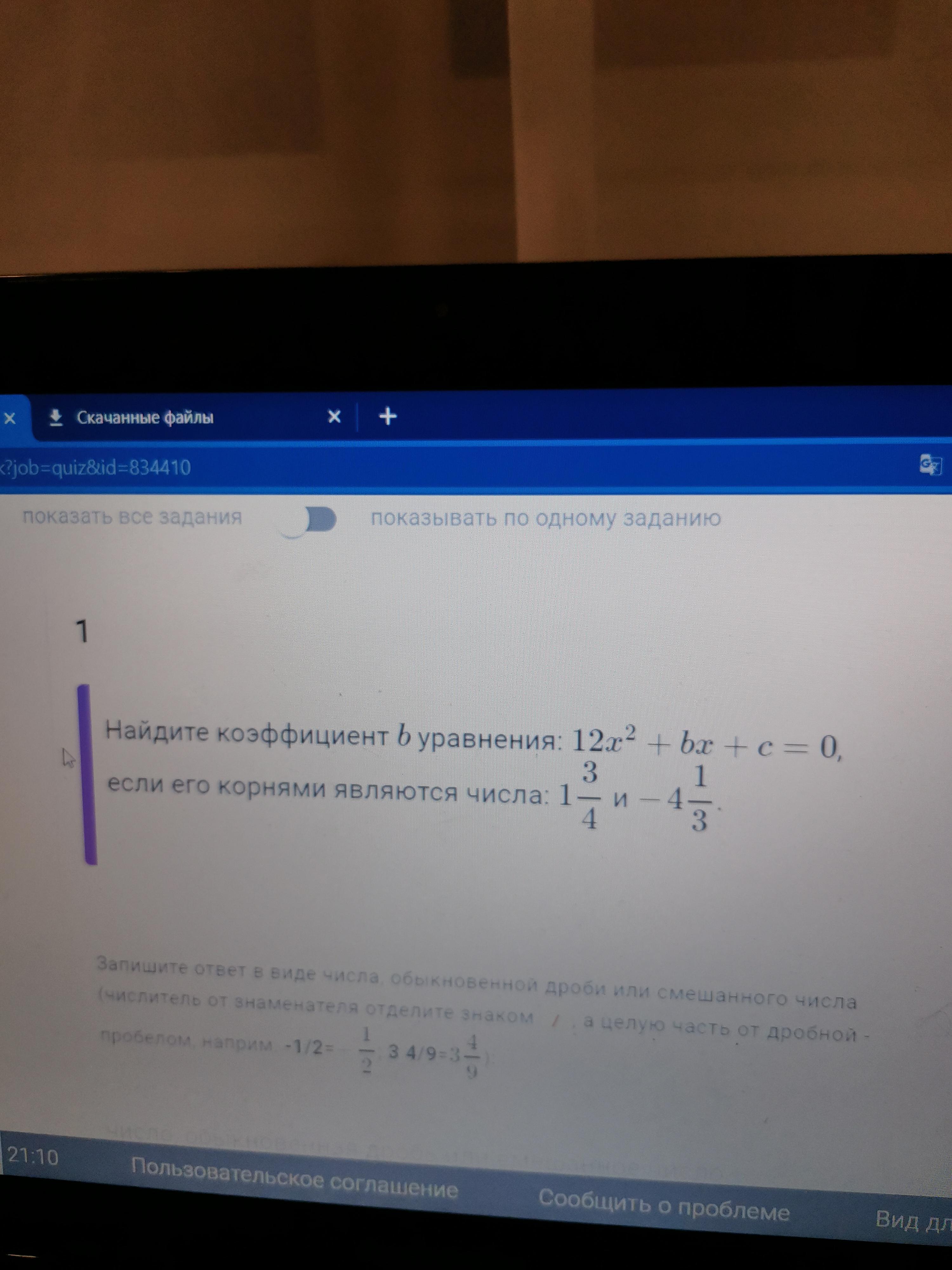
Найдите коэффициент b уравнения 12x'2 + bx + c = 0
Если его корни 1 3/4 и -4 1/3
Приложения:
Ответы на вопрос
Ответил pox1tix2
0
Ответ:
Подставляем первый корень в уравнение:
12*(0,25^2) + b*0,25 + c = 0,
3*4*(1/16) + (b/4) + c = 0;
(3/4) + (b/4) + c = 0, домножим уравнение на 4,
3 + b + 4c = 0, (*)
Подставляем второй корень в уравнение:
12*(4/3)^2 + b*(4/3) + c = 0;
4*3*(16/9) + b*(4/3) + c = 0;
(64/3) + (4/3)*b + c = 0;
домножим уравнение на 3,
64 + 4b+ 3c = 0, (**).
У нас получилась система из двух уравнений (*) и (**)
3 + b + 4c = 0
64 + 4b + 3c = 0,
Выразим b из первого уравнения системы и подставим во второе уравнение системы:
b = -3 - 4c,
64 + 4*( -3 - 4c) + 3c = 0;
64 - 12 - 16c + 3c = 0;
52 - 13c = 0;
13c = 52,
c = 52/13 = 4.
Объяснение:
Новые вопросы
Русский язык,
2 года назад
Алгебра,
8 лет назад