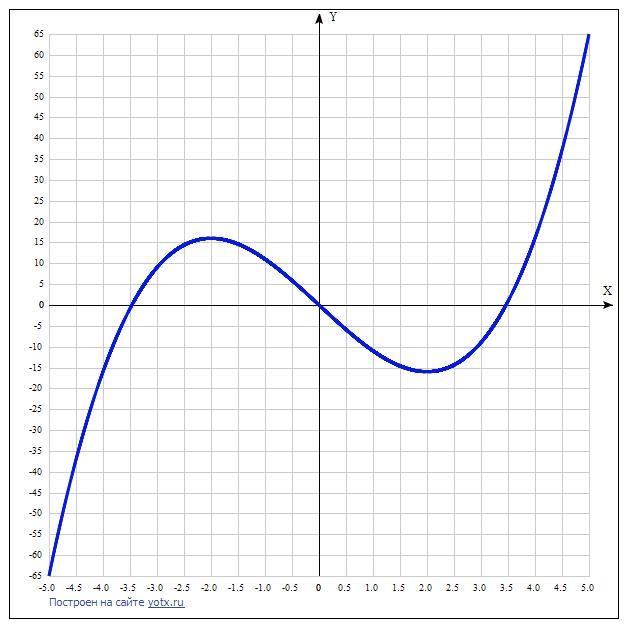
Найдите экстремумы, интервалы возрастания и убывания функции y=x³-12x и постройте её график
Ответы на вопрос
Ответил dnepr1
0
Дана функция y = x³ - 12x.
Её производная равна y' = 3х² -12.
Приравняем нулю 3х² -12 = 3(х² - 4) = 0.
Отсюда определяем 2 критические точки: х = 2 и х = -2.
Находим знаки производной на полученных промежутках.
х = -3 -2 0 2 3
y' = 15 0 -12 0 15
Где производная положительна - функция возрастает, где отрицательна - там убывает. Точки, в которых происходит смена знака и есть точки экстремума - где производная с плюса меняется на минус - точка максимума, а где с минуса на плюс - точки минимума.
• Минимум функции в точке: х = 2,
• Максимум функции в точке: х = -2.
• Возрастает на промежутках: (-∞; -2) U (2; +∞).
• Убывает на промежутке: : (-2; 2).
Приложения:
Новые вопросы