найдите число корней уравнения...., принпдлежащих промежутку (-п;3п/2)
Приложения:
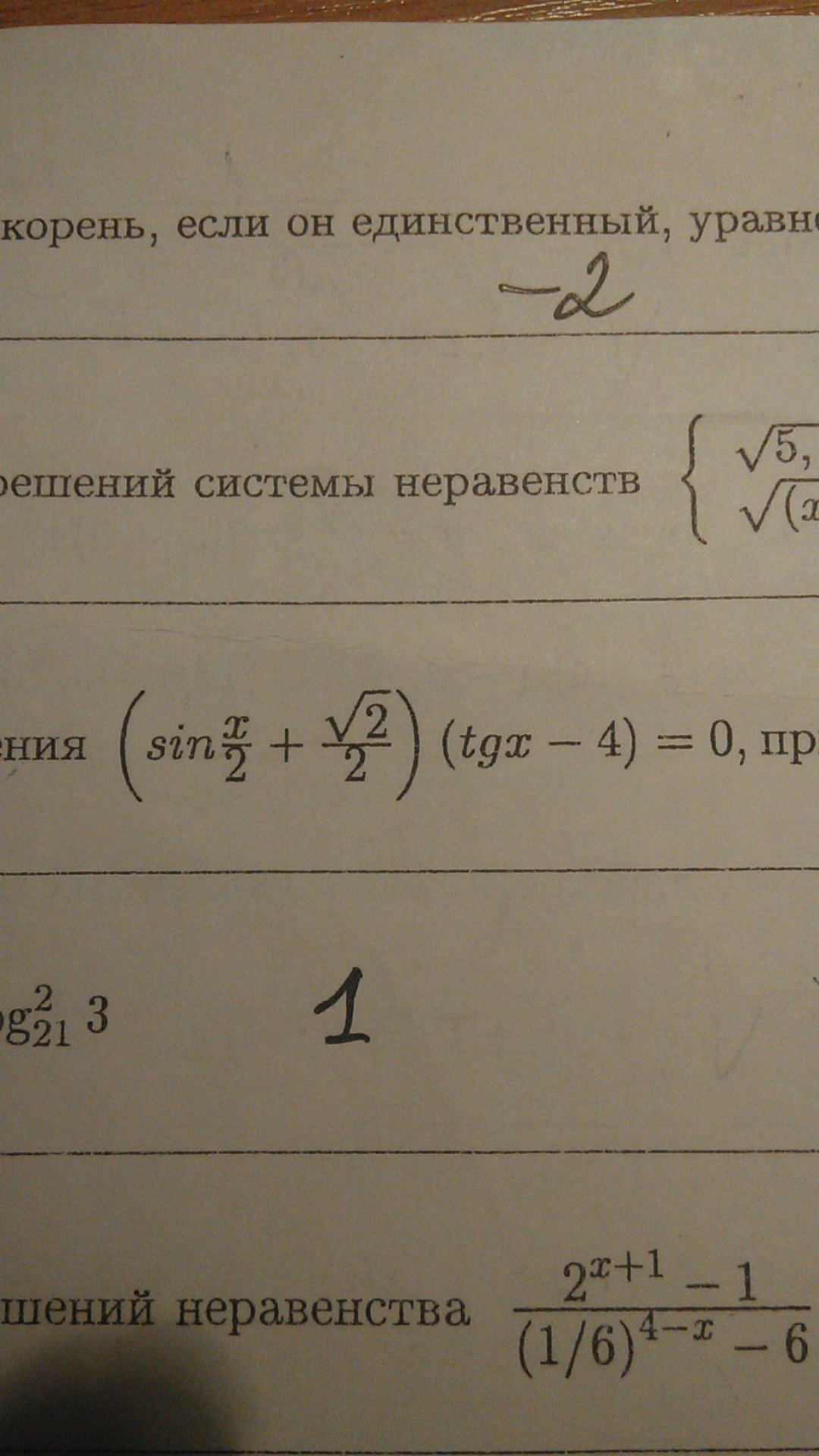
Ответы на вопрос
Ответил treez0r
0
а) Решением уравнения будет:
sin(x/2)=-√2/2, либо tgx=4, откуда
1) x/2=-π/4+2πn, n€Z
2) x/2=(π+π/4)+2πm, m€Z
3) x=arctg4+πk, k€Z
Корнями будут являться:
x1=-π/2+4πn, n€Z
x2=5π/2+4πm, m€Z
x3=arctg4+πk, k€Z.
б) x€(-π;3π/2)
1) x1.
-π<-π/2+4πn<3π/2
-π/2<4πn<2π
-1/8<n<1/2, n€Z
n=0
x=-π/2
2) x2.
-π<5π/2+4πm<3π/2
-7π/2<4πm<-π
-7/8<m<-1/4, m€Z
3) x3.
С помощью единичной окружности отберем корни:
x=-3π/2-arctg4
x=arctg4
x=3π/2-arctg4
(вроде так)
sin(x/2)=-√2/2, либо tgx=4, откуда
1) x/2=-π/4+2πn, n€Z
2) x/2=(π+π/4)+2πm, m€Z
3) x=arctg4+πk, k€Z
Корнями будут являться:
x1=-π/2+4πn, n€Z
x2=5π/2+4πm, m€Z
x3=arctg4+πk, k€Z.
б) x€(-π;3π/2)
1) x1.
-π<-π/2+4πn<3π/2
-π/2<4πn<2π
-1/8<n<1/2, n€Z
n=0
x=-π/2
2) x2.
-π<5π/2+4πm<3π/2
-7π/2<4πm<-π
-7/8<m<-1/4, m€Z
3) x3.
С помощью единичной окружности отберем корни:
x=-3π/2-arctg4
x=arctg4
x=3π/2-arctg4
(вроде так)
Новые вопросы