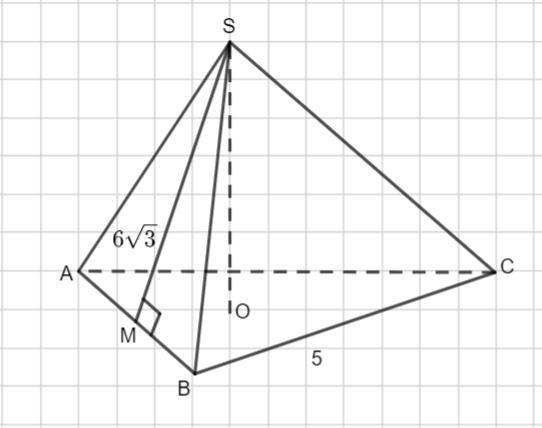
Геометрия, вопрос задал kirill8937670967 , 6 лет назад

Найди площадь полной поверхности правильной треугольной пирамиды, высота боковой грани которой равна 6√3, а сторона основания 5

orjabinina: S(полн)=S(бок)+S(осн)=1/2*Р*а+(а₃)²√3/4,
где а-апофема боковой грани ,
а₃-сторона основания правильного треугольника.
S(полн)=1/2*15*6√3+25√3/4=45√3+6,25√3=51,25√3(ед²)

Ответы на вопрос

Ответил lilyatomach

1

Ответ:

$\dfrac{205\sqrt{3} }{4}$ кв. ед. - площадь полной поверхности пирамиды.

Объяснение:

По условию задана правильная треугольная пирамида. Высота боковой грани SM= 6√3 , cтороны AB = BC =AC = 5.

Найдем площадь полной поверхности данной пирамиды.

Площадь полной поверхности пирамиды равна сумме площадей основания и боковой поверхности.

Площадь равностороннего треугольника определяется по формуле:

$S=\dfrac{a^{2}\sqrt{3} }{4} , a-$ сторона треугольника.

$S=\dfrac{5^{2}\sqrt{3} }{4} =\dfrac{25\sqrt{3} }{4}$ кв. ед.

Площадь боковой поверхности правильной пирамиды определяется по формуле

$S=\dfrac{1}{2} P\cdot l,$ где Р - периметр основания , l- апофема

Апофема - это высота боковой грани. То есть SM= 6√3.

$P= 3\cdot 5 =15$

Тогда площадь боковой поверхности

$S=\dfrac{1}{2} \cdot 15\cdot 6\sqrt{3} =15\cdot 3\sqrt{3} =45\sqrt{3}$ кв. ед.

Площадь полной поверхности пирамиды равна

$S=\dfrac{25\sqrt{3} }{4}+45\sqrt{3} =\dfrac{25\sqrt{3} +180\sqrt{3} }{4}=\dfrac{205\sqrt{3} }{4}$ кв. ед.

Приложения:

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

Из предложений 16—19 выпишите слово, в котором правописание приставки зависит от глухости/звонкости звука, обозначаемого следующей после приставки буквой. — (16)Много нельзя, — предупредила бабушка.

Қазақ тiлi, 1 год назад

люди кто такая Роза Бағланова...

Математика, 6 лет назад

помогите,прошу.Меня мама убьёт если не сделаю:((...

Английский язык, 6 лет назад

Hi Damir how s spain)(привет Дамир что ты делаешь)( hello Zhaniya We re having a wonderful time)(привет жания я провожу время на улеце. надо написать по казахскому...

Математика, 8 лет назад

Расстояние между двумя пристанями 60 км. лодка преодолевает это расстояние между ними туда и обратно за 4,5 ч. найти собственную скорость лодки, есть скорость течения реки равна 3 км/ч...

История, 8 лет назад

Что говорит о нежелании русских князей признать первенство крестоносцев...