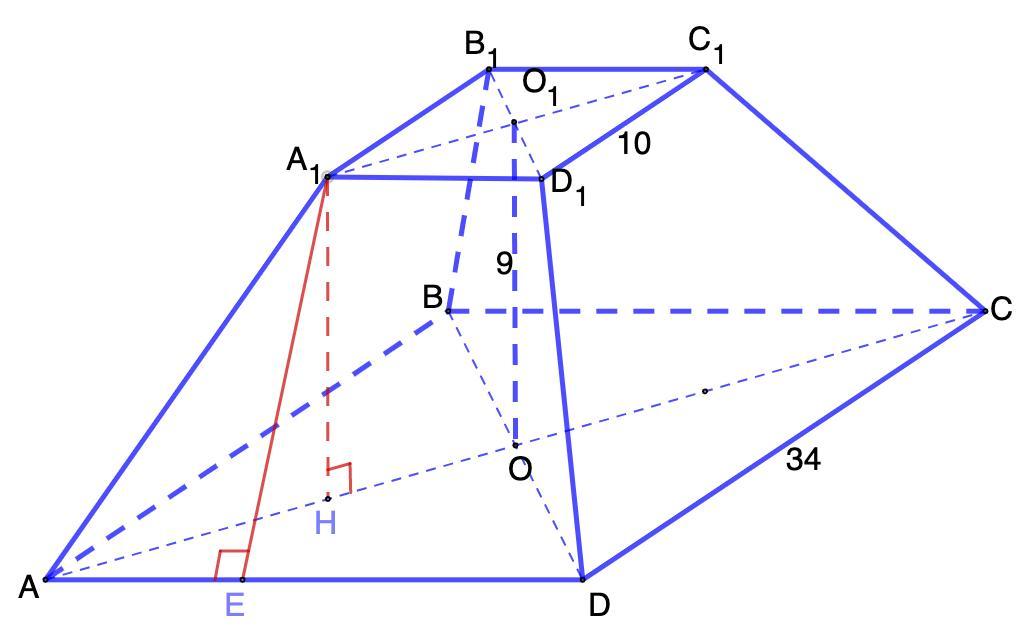
Найди площадь боковой поверхности правильной четырёхугольной усечённой пирамиды, стороны оснований которой равны 34 и 10, а высота - 9
Ответы на вопрос
Ответ:
Площадь боковой поверхности правильной четырёхугольной усечённой пирамиды равна 1320 ед.².
Объяснение:
Найти площадь боковой поверхности правильной четырёхугольной усечённой пирамиды, стороны оснований которой равны 34 и 10, а высота - 9.
Дано: ABCDA₁B₁C₁D₁ - правильная усеченная пирамида.
АВ = 34; А₁В₁ = 10; ОО₁ = 9.
Найти: S боковой поверхности.
Решение:
Пирамида правильная, значит в основаниях - квадраты.
Боковая поверхность состоит из четырех равнобедренных трпеций.
1. АВСD - квадрат.
Диагональ квадрата равна:
d = a√2, где а - сторона квадрата.
АС - диагональ.
АС = 34√2;
А₁В₁С₁D₁ - квадрат.
А₁С₁ - диагональ.
АС = 10√2;
2. Рассмотрим АА₁СС₁ - равнобедренная трапеция.
- Высота, опущенная из вершины тупого угла равнобедренной трапеции на большее основание, делит его на части, меньшая из которых равна полуразности оснований.
⇒ АН = (АС - А₁С₁) : 2 = (34√2 - 10√2) : 2 = 12√2
3. Рассмотрим ΔАА₁Н - прямоугольный.
АН = 12√2; А₁Н = 9.
По теореме Пифагора:
АА₁² = АН² + А₁Н² = 288 + 81 =369
АА₁ = √369
4. Рассмотрим ΔАА₁DD₁ - равнобедренная трапеция.
Проведем А₁Е ⊥ AD.
АЕ = (AD - A₁D₁) : 2 = (34 - 10) : 2 = 12
5. Рассмотрим ΔАА₁Е - прямоугольный.
По теореме Пифагора:
А₁Е² = АА₁² - АЕ² = 369 - 144 = 225
А₁Е = √225 = 15
6. Найдем S (AA₁DD₁):
- Площадь трапеции равна произведению полусуммы оснований на высоту.
7. Найдем площадь боковой поверхности:
Sбок. = S (AA₁DD₁) · 4 = 330 · 4 = 1320 (ед.²)
Площадь боковой поверхности правильной четырёхугольной усечённой пирамиды равна 1320 ед.².