наверное под буквой а можно не делать...​

Ответ:

1 задание под пунктом б расписано в объяснении

Пошаговое объяснение:

1б

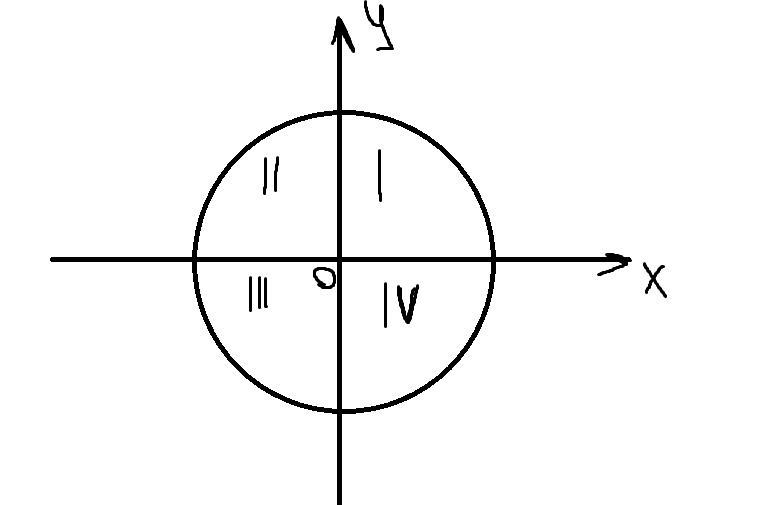
cos - абсцисса (x)

sin - ордината (y)

Т.к. в 1 четверти x > 0; y > 0 => sin > 0; cos > 0; tg > 0; ctg > 0;

2 четверть: x < 0; y > 0 => sin > 0; cos < 0; tg < 0; ctg < 0;

3 четверть: x < 0; y < 0 => sin < 0; cos < 0; tg > 0; ctg > 0;

4 четверть: x > 0; y < 0 => sin < 0; cos > 0; tg < 0; ctg < 0;

2