Алгебра, вопрос задал Аноним , 6 лет назад

Напишите уравнения касательной функции f(x) в точке с абцссой Хо

Приложения:

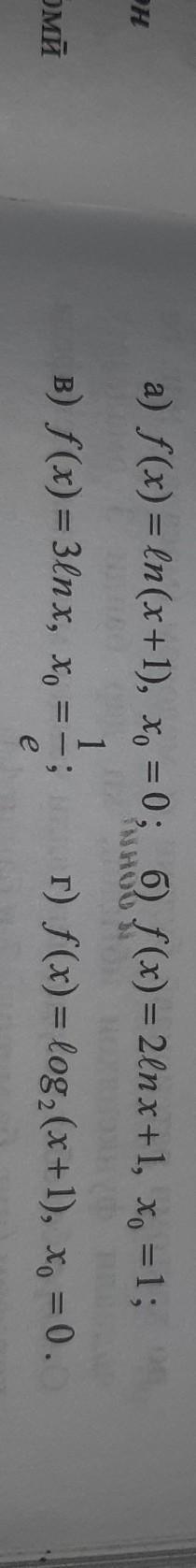
Ответы на вопрос

Ответил Miroslava227

0

Ответ:

$f(x) = f(x_0) + f'(x_0)(x - x_0)$

a

$f(x) = ln(x + 1) \\ x_0 = 0$

$f(0) = ln(1) = 0$

$f'(x) = \frac{1}{x + 1} \\$

$f'(0) = \frac{1}{1} = 1 \\$

$f(x) = 0 + 1(x - 0) = x$

б

$f(x) = 2 ln(x) + 1 \\ x_0 = 1$

$f(1) = 0 + 1 = 1$

$f'(x) = \frac{2}{x} \\$

$f'(1) = 2$

$f(x) = 1 + 2(x - 1) = 1 + 2x - 2 = \\ = 2x - 1$

в

$f(x) = 3 ln(x) \\ x_0 = \frac{1}{e} = {e}^{ - 1} \\$

$f( \frac{1}{e} ) = 3 ln(e {}^{ - 1} ) = - 3 \\$

$f'(x) = \frac{3}{x} \\$

$f'( \frac{1}{e} ) = 3e \\$

$f(x) = - 3 + 3e(x - \frac{1}{e} ) = \\ = - 3 + 3ex - 3 = 3ex - 6$

г

$f(x) = log_{2}(x + 1) \\ x_0 = 0$

$f(0) = 0$

$f'(x) = \frac{1}{ ln(2) (x + 1)} \\$

$f'(0) = \frac{1}{ ln(2) } \\$

$f(x) = 0 + \frac{1}{ ln(2) } (x - 0) = \frac{x}{ ln(2) } \\$

Предыдущий вопрос

Следующий вопрос

Новые вопросы

Русский язык, 1 год назад

Помогите,пожалуйста!В стихотворении Н.Рубцова есть такие строчки: "Люблю твои избушки и цветы, И небеса,горящие от зноя..." Вопрос:почему не ставится запятая после слова избушки?Ведь по правилам...

Математика, 1 год назад

помогите решить задачу. Велосипедист проезжает путь из города в посёлок ,со скоростью 17км/ч, за 5часов. Сколько времени потребуется пешеходу, что бы пройти этот же путь, если он движется со...

Алгебра, 6 лет назад

восьмий член геометричної прогресії дорівнює 7, а дев'ятий її член дорівнює 11. Визначне знаменник цієї прогресії...

Литература, 6 лет назад

Змінившись пiд чарівним капелюхом, Мумі-троль назвався друзям... друзям... О Король Каліфорнії О O Великий та страшний Муммі ОЧарівний троль О Мара...

Алгебра, 8 лет назад

найдите значение выражения 1/3√2-1-1/3√2+1...

Математика, 8 лет назад

В букете 5 гвоздик , 13 веток жасмина и несколько роз.Какую часть букета составляют розы, есле в букете 27 цветов ( тема простые дроби доля...